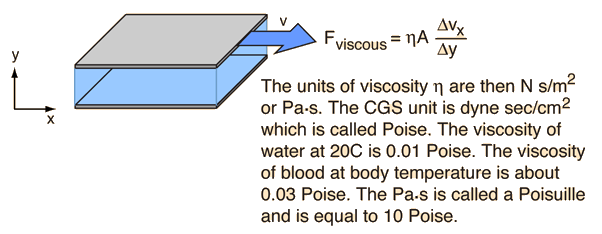
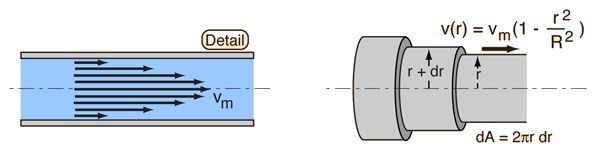
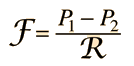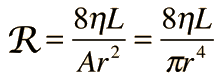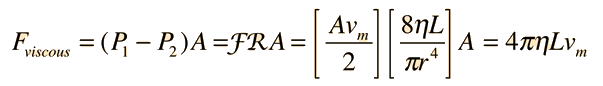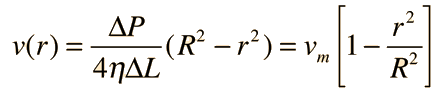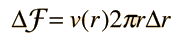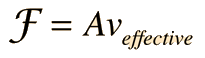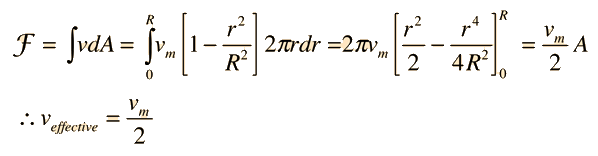Laminar Flow

The resistance to flow in a liquid can be characterized in terms of the viscosity of the fluid if the flow is smooth. In the case of a moving plate in a liquid, it is found that there is a layer or lamina which moves with the plate, and a layer which is essentially stationary if it is next to a stationary plate.

There is a gradient of velocity as you move from the stationary to the moving plate, and the liquid tends to move in layers with successively higher speed. This is called laminar flow, or sometimes "streamlined" flow. Viscous resistance to flow can be modeled for laminar flow, but if the lamina break up into turbulence, it is very difficult to characterize the fluid flow.

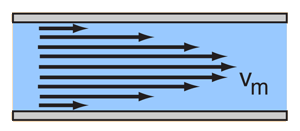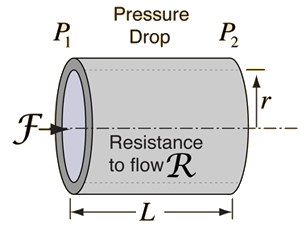
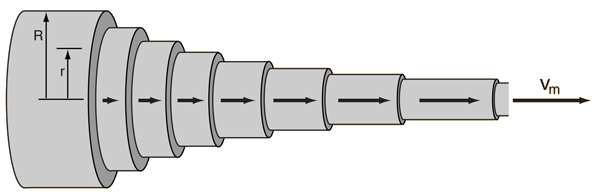
The common application of laminar flow would be in the smooth flow of a viscous liquid through a tube or pipe. In that case, the velocity of flow varies from zero at the walls to a maximum along the centerline of the vessel. The flow profile of laminar flow in a tube can be calculated by dividing the flow into thin cylindrical elements and applying the viscous force to them.

One effect of viscous forces even in laminar flow is to do negative work on the fluid and reduce its mechanical energy. Since fluid pressure is a measure of fluid mechanical energy per unit volume, this negative work can be correlated with the drop in fluid pressure along the flow path. This drop in macroscopic mechanical energy can be correlated with an increase in the internal energy of the fluid, resulting in a slight increase in temperature.

Viscosity

Flow Resistance for a Tube

The flow resistance of a tube is defined from the relationship where the script F is the volume flowrate through the tube. This volume flowrate can also be expressed by

Show

where v_m is the maximum flow velocity at the center of the tube. The resistance denoted by the script R can be calculated from:

Stated in terms of a viscous resistance force,

Fluid Velocity Profile

Under conditions of laminar flow in a viscous fluid, the velocity increases toward the center of a tube.

The velocity profile as a function of radius is

Show

The fluid transported by each lamina is given by

and the summing of the contributions gives flow

Show

Effective Fluid Speed in a Tube

In order to get the net resistance to flow for laminar fluid flow through a tube, one must account for the fact that different lamina of the flow travel at different speeds and encounter different resistances.

The volume flowrate can be generally expressed by

but the effective velocity is not a simple average because of the nonlinear velocity profile. The total volume flowrate can be calculated by integration of the flow of the successive lamina.