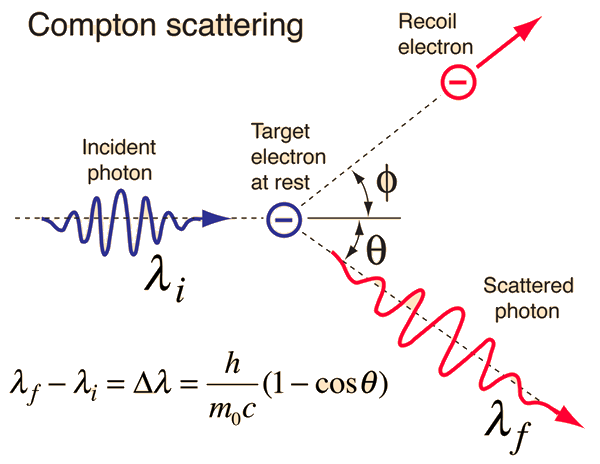
The scattering of photons from charged particles is called Compton scattering after Arthur Compton who was the first to measure photon-electron scattering in 1922. When the incoming photon gives part of its energy to the electron, then the scattered photon has lower energy and according to the Planck relationship has lower frequency and longer wavelength. The wavelength change in such scattering depends only upon the angle of scattering for a given target particle. The constant in the Compton formula above can be written
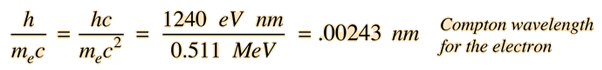
and is called the Compton wavelength for the electron. The formula presumes that the scattering occurs in the rest frame of the electron.
This exploration is designed to accept values for the input wavelength or energy and the angle of scattering. Unspecified parameters will default to the case of molybdenum K-alpha xrays scattering at 90 degrees, one of Compton's historical results. Any of these input values can be changed.
| Compton Scattering Data | Derivation of equation |
| Significance of Compton scattering |
| Extreme case of highly relativistic photon |
Great experiments of physics
Reference:
Compton
| HyperPhysics***** Quantum Physics | R Nave |