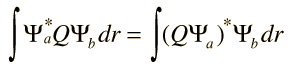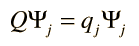The Operator Postulate
With every physical observable there is associated a mathematical operator which is used in conjunction with the wavefunction. Suppose the wavefunction associated with a definite quantized value (eigenvalue) of the observable is denoted by Ψn (an eigenfunction) and the operator is denoted by Q. The action of the operator is given by
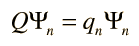
The mathematical operator Q extracts the observable value qn by operating upon the wavefunction which represents that particular state of the system. This process has implications about the nature of measurement in a quantum mechanical system. Any wavefunction for the system can be represented as a linear combination of the eigenfunctions Ψn ( see basis set postulate), so the operator Q can be used to extract a linear combination of eigenvalues multiplied by coefficients related to the probability of their being observed (see expectation value postulate).
| Discussion of operators |
Schrodinger equation concepts
Postulates of quantum mechanics
| HyperPhysics***** Quantum Physics | R Nave |