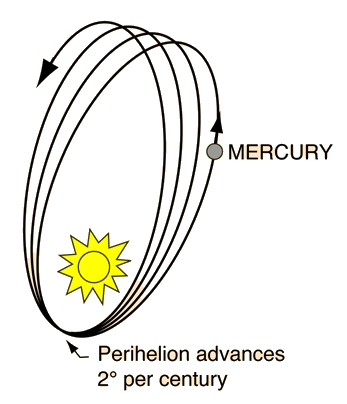
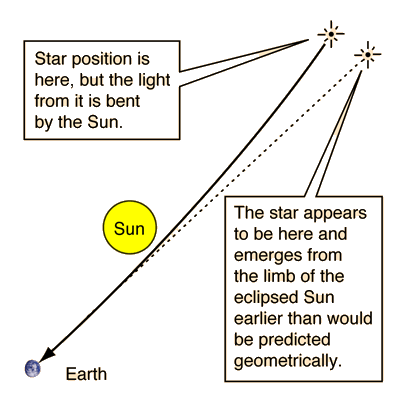
Eddington's Measurement of Light Deflection
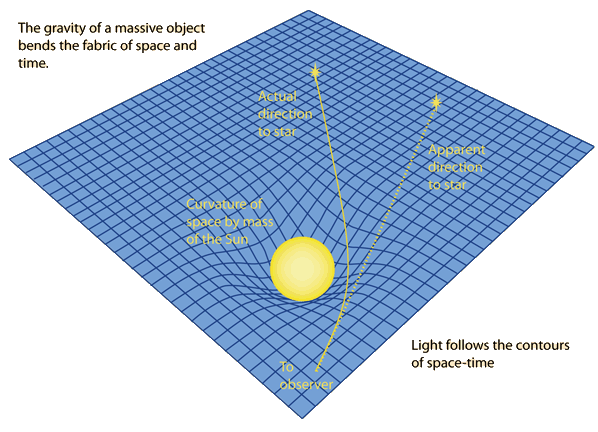
Einstein's calculations in his
newly developed general
relativity indicated that the
light from a star which just grazed
the sun should be deflected by 1.75 seconds of arc. The depiction of this bending is greatly exaggerated in the illustration above.
Einstein, writing in a German journal during World War I, suggested that during a total solar eclipse the deflection should be observable in terms of the time of emergence of a star from behind the Sun. Fraknoi, et al. comment that a copy of that paper came through neutral Holland and reached British astronomer Arthur S. Eddington. An expedition was organized to attempt to measure this deflection during the next total solar eclipse on May 29, 1919 at two locations: the island of Principe off the west coast of Africa and Sobral, Brazil. Photographs were obtained in both locations and confirmed the predicted deflection to about 20% accuracy.
Measurements during total solar eclipses have been made several times, notably by the Yerkes Observatory in 1953 and by the University of Texas in 1973. More accurate radio frequency measurements after that time became the standard approach to gravitational deflection of electromagnetic waves.
|
Index
General relativity ideas
Fraknoi, Morrison, Wolff
Ch 23 |