Simple Harmonic Motion
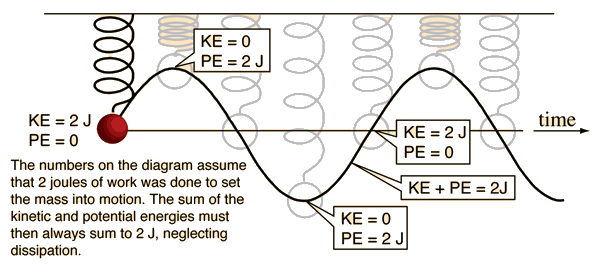
When a mass is acted upon by an elastic force which tends to bring it back to its equilibrium configuration, and when that force is proportional to the distance from equilibrium (e.g., doubles when the distance from equilibrium doubles, a Hooke's Law force), then the object will undergo simple harmonic motion when released.
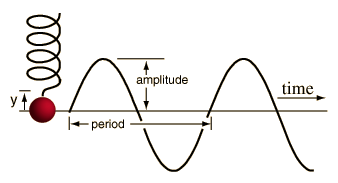 |
A mass on a spring is the standard example of such periodic motion. If the displacement of the mass is plotted as a function of time, it will trace out a pure sine wave. Energy of simple harmonic motion |
It turns out that the motion of the medium in a traveling wave is also simple harmonic motion as the wave passes a given point in the medium.
| Mathematical description |
Periodic motion concepts
| HyperPhysics***** Sound | R Nave |