Carnot Cycle

The most efficient heat engine cycle is the Carnot cycle, consisting of two isothermal processes and two adiabatic processes. The Carnot cycle can be thought of as the most efficient heat engine cycle allowed by physical laws. When the second law of thermodynamics states that not all the supplied heat in a heat engine can be used to do work, the Carnot efficiency sets the limiting value on the fraction of the heat which can be so used.

In order to approach the Carnot efficiency, the processes involved in the heat engine cycle must be reversible and involve no change in entropy. This means that the Carnot cycle is an idealization, since no real engine processes are reversible and all real physical processes involve some increase in entropy.

For = K = K the Carnot efficiency is %

The temperatures in the Carnot efficiency expression must be expressed in Kelvins. For the other temperature scales, the following conversions apply:

=K = °C = °F

=K = °C = °F

The conceptual value of the Carnot cycle is that it establishes the maximum possible efficiency for an engine cycle operating between T_H and T_C. It is not a practical engine cycle because the heat transfer into the engine in the isothermal process is too slow to be of practical value. As Schroeder puts it, "So don't bother installing a Carnot engine in your car; while it would increase your gas mileage, you would be passed on the highway by pedestrians."

Entropy and the Carnot Cycle

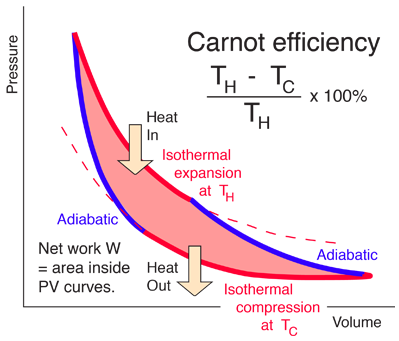The efficiency of a heat engine cycle is given by 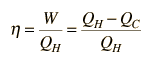For the ideal case of the Carnot cycle, this efficiency can be written

Using these two expressions together

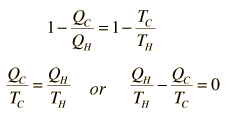
If we take Q to represent heat added to the system, then heat taken from the system will have a negative value. For the Carnot cycle

which can be generalized as an integral around a reversible cycle

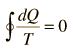Clausius Theorem

For any part of the heat engine cycle, this can be used to define a change in entropy S for the system

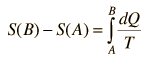
or in differential form at any point in the cycle

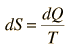
For any irreversible process, the efficiency is less than that of the Carnot cycle. This can be associated with less heat flow to the system and/or more heat flow out of the system. The inevitable result is

Clausius Inequality

Any real engine cycle will result in more entropy given to the environment than was taken from it, leading to an overall net increase in entropy.