The Clausius Theorem and Inequality

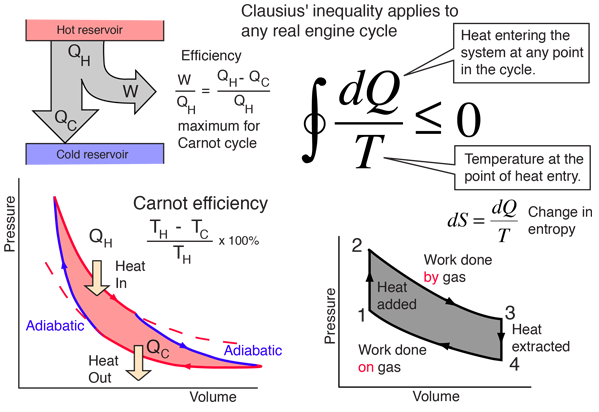
The integral in the illustration above represents the change in entropy for a complete cycle of a heat engine. Recognizing that integral as an entropy integral could be confusing because you are probably aware that the total entropy must increase for any irreversible engine cycle. But this change in entropy describes what happens to the engine itself, and carries the idea that the entropy on the output side, given to the environment, by the engine in an irreversible cycle is always greater that the entropy added to that engine. So it is consistent with the general understanding of entropy in the second law of thermodynamics, that it always increases for an irreversible process.

The equal sign in the Clausius inequality above applies only to the the ideal or Carnot cycle. Since the integral represents the net change in entropy in one complete cycle, it attributes a zero entropy change to the most efficient engine cycle, and makes it clear that entropy does not decrease even in an ideal engine cycle.

The Clausius Inequality applies to any real engine cycle and implies a negative change in entropy on the cycle. That is, the entropy given to the environment during the cycle is larger than the entropy transferred to the engine by heat from the hot reservoir. In the simplified heat engine where the heat Q_H is all added at temperature T_H, then an amount of entropy ΔS = Q_H/T_H is added to the system and must be removed to the environment to complete the cycle. In general, the engine temperature will be less than T_H for at least part of the time when heat is being added, and any temperature difference implies an irreversible process. Excess entropy is created in any irreversible process, and therefore more heat must be dumped to the cold reservoir to get rid of this entropy. This leaves less energy to do work.