Teorema de Elevación de Kutta-Joukowski
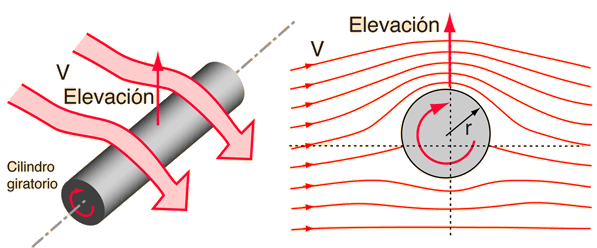
Dos antiguos científicos en la aerodinámica, Kutta en Alemania y Joukowski en Rusia, trabajaron para cuantificar la elevación obtenida por un flujo de aire sobre un cilindro giratorio. La relación de elevación es
donde ρ es la densidad del aire, V es la velocidad del flujo, y G se llama "intensidad de vórtice". La intensidad de vórice está dada por
donde ω es la velocidad angular del giro del cilindro. Esto se puede describir también como la velocidad de la superficie (velocidad Vr = ωr de la superficie asociada con la rotación) multiplicada por la circunferencia del cilindro.
Como todas las elevaciones aerodinámicas, esto parece un poco misterioso, pero lo podemos ver en términos de redireccionamiento del flujo del aire. Si el cilindro atrapa algo del aire en la capa límite de la superficie del cilindro y lo lleva a su alrededor e impulsándolo hacia abajo, entonces le ha dado un momento hacia abajo. Eso puede actuar para dar al cilindro un momento hacia arriba, de acuerdo con el principio de conservación del momento. Otro enfoque es decir, que se ha ejercido sobre el aire, una componente de la fuerza hacia abajo y bajo la tercera ley de Newton debe haber una fuerza hacia arriba sobre el cilindro. Otro enfoque mas, es decir que la parte superior del cilindro está ayudando a la corriente de aire, acelerando el flujo sobre la parte superior del cilindro. Entonces por la ecuación de Bernoulli, la presión sobre la parte superior del cilindro disminuye, proporcionandole una elevación efectiva.
Conceptos de Bernoulli
Referencias
Eastlake

NASA
Aerodynamics
| HyperPhysics*****Mecánica*****Fluidos | M Olmo R Nave |