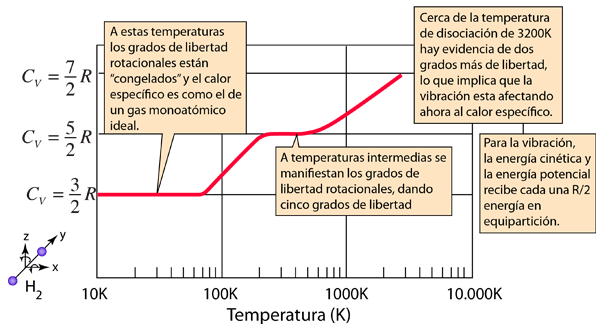
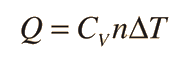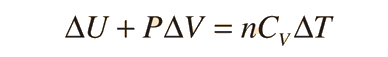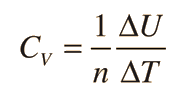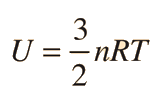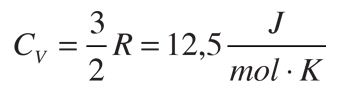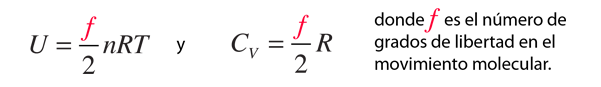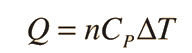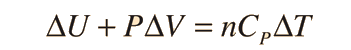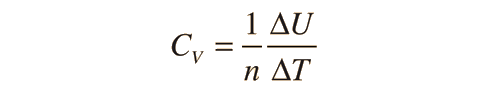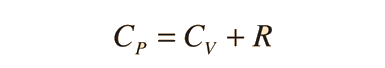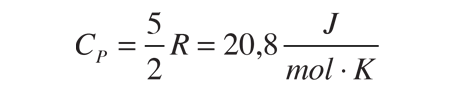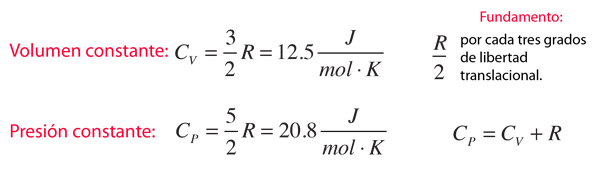Calores Específicos de Gases
Los calores específicos de gases se expresan normalmente como calores específicos molares. En un gas ideal monoatómico, la energía interna está toda ella en forma de energía cinética, y la teoría cinética proporciona la expresión de esa energía, respecto de la temperatura cinética. La expresión de la energía cinética es
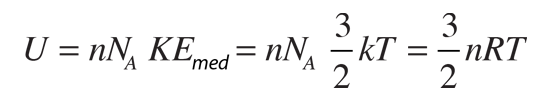
En los gases se definen dos calores específicos, uno a volumen constante (CV) y otra a presión constante (CP). Para un proceso a volumen constante con un gas ideal monoatómico, la primera ley de la termodinámica da:
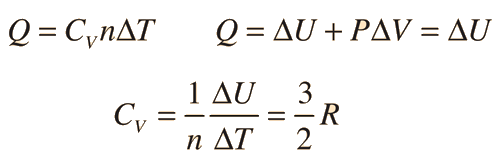 | Caso Mas General |
Una aplicación mas detallada de la ley de gas ideal y la primera ley, lo da la fórmula
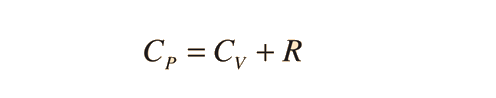 | Mostrar |
La proporción entre calores específicos γ = CP/CV, es un factor en los procesos de los motores adiabáticos, y en la determinación de la velocidad del sonido en un gas. Esta proporción es γ = 1,66 para un gas monoatómico ideal, y γ = 1,4 para el aire, que es predominantemente un gas diatómico.
Conceptos sobre la Ley de Gas
Conceptos sobre Teoría Cinética
| HyperPhysics*****Termodinámica | M Olmo R Nave |