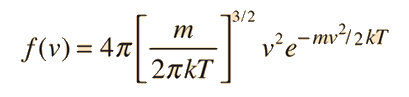Temperatura Cinética

La expresión para la presión de gas desarrollada desde la teoría cinética, relaciona la presión y el volumen del gas con la energía cinética molecular media. La comparación con la ley de gas ideal nos conduce a una temperatura llamada algunas veces temperatura cinética.

Mostrar

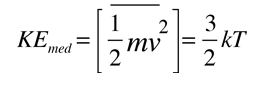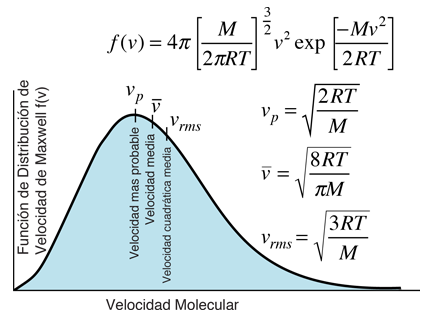
Es importante señalar que la energía cinética media que se utiliza aquí, se limita a la energía cinética de traslación de las moléculas. Es decir, son tratadas como masas puntuales y no se tiene en cuenta los grados de libertad internos, tales como la rotación molecular y la vibración. Esta distinción es muy importante cuando se tratan temas como los calores específicos de gases. Al tratar de evaluar el calor específico, se debe tener en cuenta toda la energía que poseen las moléculas, y la temperatura tal como ordinariamente se mide no tiene en cuenta la rotación y vibración molecular. La temperatura cinética es la variable necesaria para temas como la transferencia de calor, ya que es la energía cinética de traslación, que conduce la transferencia de energía, desde zonas calientes (mayor temperatura cinética, mayores velocidades moleculares), a zonas frías (menores velocidades moleculares), en una transferencia colisional directa.

Velocidades Moleculares

Cálculo

Distribución de Velocidad de Maxwell

De esta función se pueden calcular varias velocidades moleculares características, y cosas tales como, qué fracción de las moléculas tienen velocidades superiores a un cierto valor a una temperatura dada. También tiene que ver con muchos tipos de fenómenos. Cálculo

Note que M es la masa molar y que en la expresión se usa la constante de gas R. Si se hubiera usado en su lugar la masa m de una molécula individual, la expresión sería la misma excepto que contendría la constante de Boltzmann k, en vez de la constante de gas molar R.

Cálculo de la Velocidad Molecular

La distribución de velocidades en las moléculas de un gas ideal está dada por

El cálculo de la velocidad molecular depende de la masa molecular y de la temperatura. Para una masa m= uma M= kg/mol y temperatura T=K T= C se pueden calcular las tres velocidades características. La masa molecular media nominal del aire seco es 29 uma.

Velocidad mas probable= v_p = m/s = km/hr = mi/hr
Velocidad Media==m/s = km/hr = mi/hr
Velocidad RMS = v_rms = m/s = km/hr = mi/hr

Desarrollo de la Distribución de Boltzmann

Cuando el número de partículas es grande, el método estadístico viene a ser la forma mas precisa de estudiar la naturaleza. De modo que esperamos que esos tres valores de velocidades de las moléculas de un gas, serán de hecho la distribución mas probable, puesto que estamos tratando con un número de partículas en el rango del número de Avogadro. Pero esta distribución mas probable (la distribución de Maxwell-Boltzmann) está sujeta a limitaciones, a saber; el número de partículas es constante, y la energía total es constante (conservación de la energía). El cálculo con la mayor precisión de la distribución de probabilidad sujetas a estas limitaciones en general, supone una ardua tarea matemática (ver por ejemplo Richtmyer, et al.). Una manera de abordar la solución de una forma mas intuitiva, es enfrentarlo con un problema físico que conocemos -llamado física de la atmósfera bajo la influencia de la gravedad-, como se refleja en la fórmula barométrica. El siguiente estudio sigue el desarrollo de Rohlf.

En este enfoque, usamos el hecho de que la energía cinética media de las moléculas, la podemos expresar en función de la temperatura cinética. Además sabemos que en este caso, la conservación de la energía implica exactamente, un equilibrio entre la energía cinética y la energía potencial gravitacional, siempre que tratemos a la atmósfera como un gas ideal.

De la expresión de temperatua cinética

tenemos una descripción de un sistema de gas ideal, que se puede usar para ayudar a desarrollar un argumento plausible para la distribución de velocidades de Maxwell. Los pasos en este procesos son como sigue:

Para una dirección en el espacio este proceso conduce a la expresión:

y cuando se incluyen todas las direcciones de la velocidad, viene a convertirse en la fórmula de la Distribución de velocidad de Maxwell:

¿Por Que esta Fórmula es Inexacta para Velocidades mas Altas, Mientras que la Anterior No lo es?

Debería notarse que aunque usamos una situación física dependiente de la gravedad para obtener la distribución de velocidad, esta no aparece en el resultado final. Es decir, el resultado obtenido es general, no contiene g. La fórmula barométrica se usó simplemente como un modelo para obtener la distribución de velocidad con las limitaciones de la energía y el número de partículas.