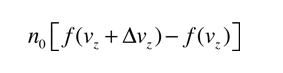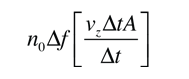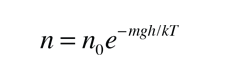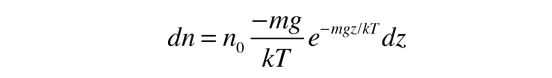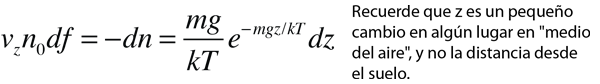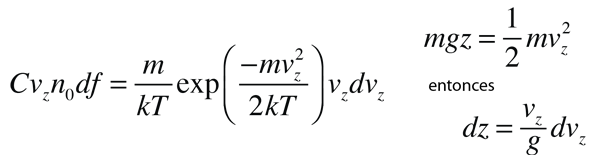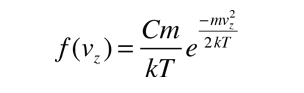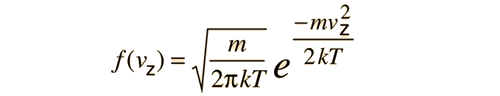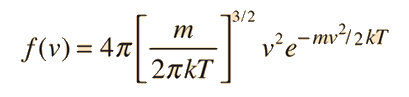Relación de la Velocidad de Partícula con la Altura
Las moléculas que finalmente están mas alta en la atmósfera, lo son porque poseen una mayor energía cinética para convertirla en energía potencial gravitacional en alguna escala de tiempo. (No importa el hecho de los miles de millones de colisiones en su camino hacia esa altura. En una escala de tiempo muy corta entre colisiones, algunas alcanzarán incrementalmente mas altura que otras, desde sus puntos de partidas. Aquí consideramos esa incremental ganancia de altura.)
Si tenemos una población de partículas que tienen suficiente energía para llegar a la altura z:
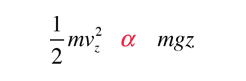
entonces, la población con una velocidad un poco más alta, puede llegar un poco más alto.
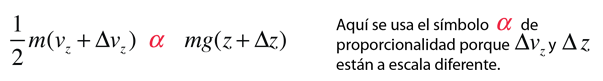
Estas consideraciones de energía, deben ser la causa de la diferencia de población con la altura, que se observa en la fórmula barométrica.
| Volver al Estudio del Desarrollo de la Distribución de Velocidades de Maxwell |
| Ir hacia la Relación del Flujo de Partículas con la Distribución de Velocidades. |
Conceptos sobre la Ley de Gas
Conceptos sobre Teoría Cinética
| HyperPhysics*****Calor y Termodinámica | M Olmo R Nave |