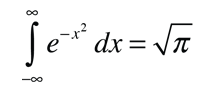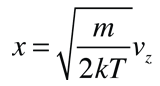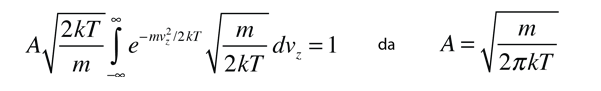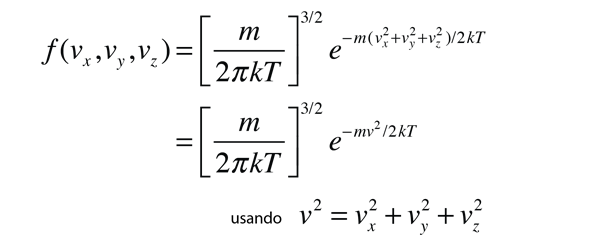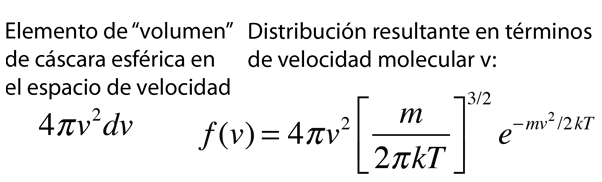Distribución de Velocidades de Maxwell Directamente de la Distribución de Boltzmann
La distribución de Boltzmann es fundamental para nuestra comprensión del fenómeno molecular clásico, que nos dice que la probabilidad de encontrar una molécula cualquiera con una energía E, disminuye exponencialmente con la energía, es decir una molécula cualquiera es muy poco probable que agarre mucho más que la cuota media de la energía total disponible para todas las moléculas. Matemáticamente, la distribución de Boltzmann se puede escribir en la forma
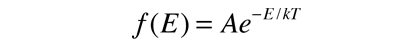
Esta distribución se puede hacer posible mediante un ejemplo numérico, particularmente cuando se pone en forma gráfica, pero el desarrollo matemático riguroso de Boltzmann se mantiene como un importante logro en las matemáticas de la física. Vamos a tomarlo como un postulado aquí y demostrar que la distribución de velocidades de Maxwell se desprende de ella.
Si esta distribución se aplica a una sola dirección de la velocidad de una molécula en un gas ideal, viene a ser
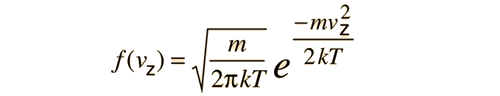 |
|
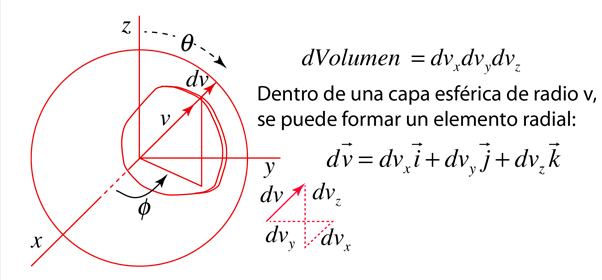
La conversión de esta fórmula en otra que exprese la probabilidad en función de las velocidades en tres dimensiones, da como resultado la distribución de velocidades de Maxwell:
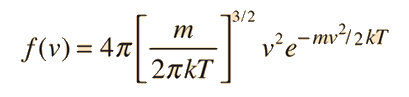
Los pasos a seguir en esta conversión son
| Conversión a Probabilidad en tres Dimensiones |
| Suma sobre todas las Direcciones Espaciales |
Conceptos sobre Teoría Cinética
| HyperPhysics*****Calor y Termodinámica | M Olmo R Nave |