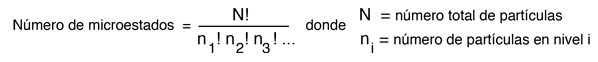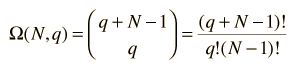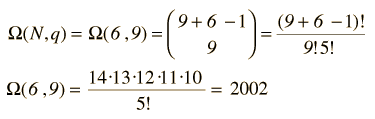 |
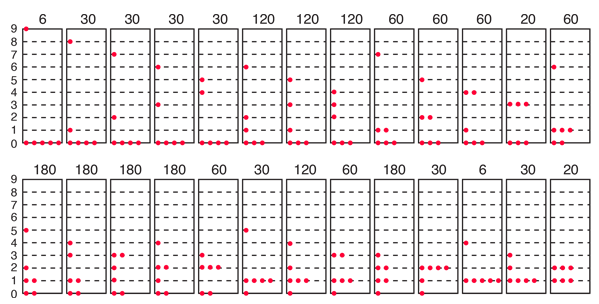
¿De cuantas maneras se pueden distribuir 9 unidades de energía, entre 6 idénticas?
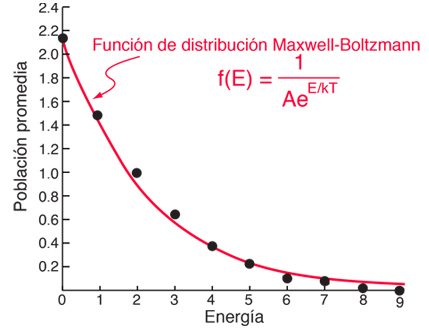
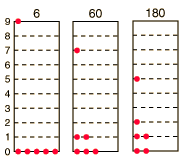
Las tres distribuciones de partículas a la izquierda tienen cada una la misma energía, el mismo tipo de partículas, y el mismo número de partículas, sin embargo, la distribución de la derecha tiene 30 veces más probabilidades que la de la izquierda. ¿Por qué es esto?. En las partículas distinguibles que se presumen en la distribución de Maxwell-Boltzmann, importa no sólo cuántas partículas hay en cada estado, sino qué partículas se encuentran en cada estado.
|
Blatt utiliza el término "macroestado", para describir la caracterización del sistema que da justo el número de partículas en cada estado; el diagrama de arriba muestra tres de los 26 macroestados posibles para este sistema. El término "microestado" se utiliza para la caracterización más detallada en la que se da el nivel de energía específico para cada partícula. El macroestado de la izquierda tiene sólo 6 microestados, porque sólo hay 6 maneras de poner una partícula en el nivel 9 y las otras 5 en el nivel 0. Pero hay 180 maneras de lograr el macroestado de la derecha, así que si cada distribución se presume que es igualmente probable, entonces el sistema es 30 veces más probable que se encuentre en el macroestado de la derecha.
El número de formas distinguibles de producir cada distribución está dada por
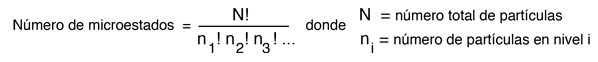
Así que para los tres macroestados de la imagen de arriba, los números de microestados son

(Recuérdese que 0!=1, de modo que los estados desocupados no afectan al cálculo.)
Ahora, para establecer la función de distribución para el número de partículas en cada estado de energía, se debe promediar el número de partículas en cada estado, sobre todos los microestados. Para cada macroestado, el número de partículas en un nivel de energía dado, se multiplica por el número de microestados. La suma de estos productos, se divide por el número total de microestados, que es 2002 en este caso.

El número de microestados (la multiplicidad W) para q unidades de energía, entre N estados igualmente probables, se puede evaluar matemáticamente de la expresión
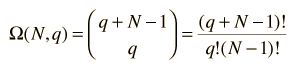
que para este caso viene a ser
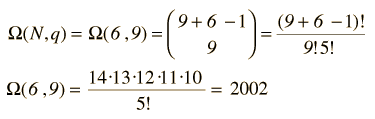
|
Índice
Referencia
Blatt
Cap. 11 |