|
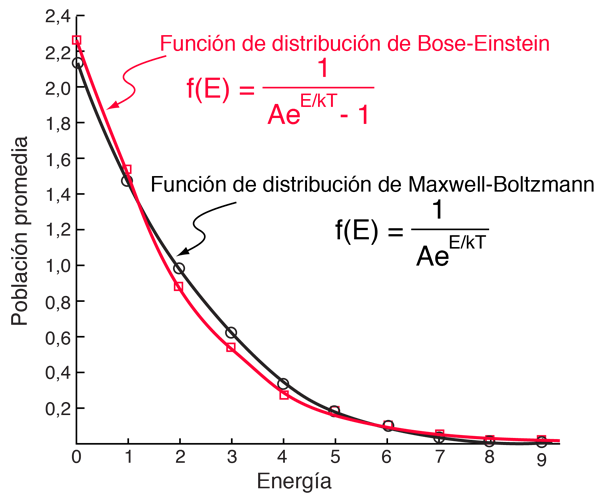
¿De cuantas maneras se pueden distribuir 9 unidades de energía, entre 6 fermiones idénticos e indistinguibles?Las tres distribuciones de partículas de la izquierda tienen cada una la misma energía, el mismo tipo de partículas, y el mismo número de partículas. Si las partículas fueran partículas distinguibles y estuvieran descritas por la estadística de Maxwell-Boltzmann, entonces la distribución de la derecha tendrían 30 veces más probabilidades que la de la izquierda, porque hay 30 maneras distinguibles de producirlas. Pero si son bosones indistinguibles, los tres estados son igualmente probables, y dan una ponderación estadística de 1. Esto significa que en lugar de 2002 microestados distinguibles derivados de 26 macroestados, sólo habría 26 estados. |
La evaluación de la ocupación promedio de cada estado de energía, es mucho más simple que en el ejemplo de Maxwell-Boltzmann puesto que cada macroestado tiene un peso de 1. La ocupación promedio es justo la suma de los números de partículas en un estado de energía dado sobre todas las 26 distribuciones, dividido por 26.
| Evaluar el Promedio de Cada Estado de Energía | Comparar con el Ejemplo de Maxwell-Boltzmann |
Referencia
Blatt
Cap. 11
| HyperPhysics*****Física Cuántica | M Olmo R Nave |