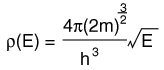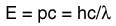La Distribución de Energía

La distribución de una cantidad fija de energía entre un número de partículas idénticas, depende de la densidad de estados de energía disponibles, y la probabilidad de que sea ocupado un estado dado. La probabilidad de que sea ocupado un estado de energía determinado, está dada por la función de distribución, pero si existen más estados de energía disponibles en un intervalo de energía dado, entonces, esto le dará un mayor peso a la probabilidad para ese intervalo de energía.

La Densidad de Estados

La distribución de energía entre partículas idénticas, depende en parte de cuantos estados hay disponible en un intervalo de energía dado. Esta densidad de estados como función de la energía, da el número de estados por unidad de volumen en un intervalo de energía. El término "peso estadístico" se utiliza a veces como sinónimo, en particular en situaciones en donde los estados disponibles son discretos. Las limitaciones físicas sobre las partículas, determinan la forma de la función de densidad de estados.

Para los electrones en un metal, la densidad de estados proviene de la naturaleza ondulatoria de los electrones en el tipo característico de la "partícula en una caja". Mostrar

Para los fotones donde la relación entre la energía y la longitud de onda es la densidad de estados es Mostrar

Distribución de Energía

Distinguibilidad de Partículas

Las distribuciones de Einstein-Bose y Fermi-Dirac difieren de la clásica distribución de Maxwell-Boltzmann, porque las partículas que describen son indistinguibles.

Las partículas se consideran que son indistinguibles, si sus paquetes de ondas se solapan significativamente. Este tipo de consideración viene del hecho, de que de acuerdo con la hipótesis de De Broglie, todas las partículas tienen propiedades características de onda. Dos partículas se pueden considerar distinguibles, si su separación es grande en comparación con su longitud de onda de De Broglie.

Por ejemplo, la condición de distinguibilidad en las moléculas de un gas ideal en condiciones normales, se cumple. Para el gas oxígeno en STP, las moléculas tienen una separación del orden de 3 nm y las longitudes de onda de De Broglie, son del orden de 0,03 nm, un factor de cien mas pequeña. Por otra parte, dos electrones en la primera capa de un átomo, son inherentemente indistinguibles debido al gran solapamiento de sus funciones de onda.