Densidad de Energía de los Electrones

El comportamiento de los electrones en los sólidos depende de la distribución de energía entre los electrones:

Como los electrones son fermiones, la función de distribución es la distribución de Fermi-Dirac

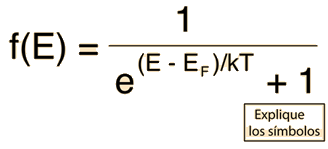
Esta distribución determina la probabilidad de que sea ocupado un estado de energía dado, pero debe ser multiplicado por la densidad de funciones de estados, para ponderar la probabability por el número de estados disponibles a una determinada energía.

La determinación de cuántas maneras hay de obtener una energía en un rango de energía incremental dE, puede ser abordada mediante la partícula en una caja de la mecánica cuántica. La energía para una caja de pared infinita es

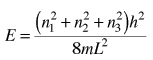
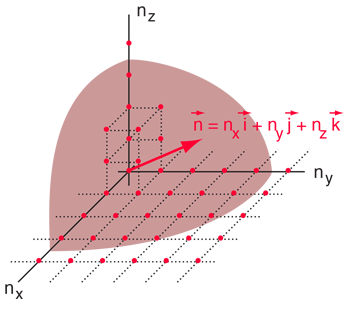
Esquema de Rayleigh para los modos de conteo. De Richtmyer, et al.

Del tratamiento de los "números cuánticos" n como un espacio, en el que un conjunto dado de n valores, determina un punto en ese espacio, se puede argumentar que el número de estados posibles es proporcional al "volumen" en el "espacio-n". Es conveniente definir un radio R en el espacio-n:

La energía puede ser expresada en términos de R, y viceversa.

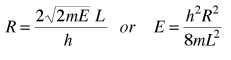
El espacio-n asociado con la partícula-en-una-caja, involucra sólo valores positivos de n, por lo que el volumen debe ser dividido por 8. A continuación, debe multiplicarse por 2 para tener en cuenta los dos posibles valores del espín del electrón. El número de valores es por tanto

El número de estados por unidad de volumen es

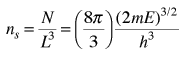
La densidad de estados final en función de la energía, es entonces la derivada de esta población con respecto a la energía

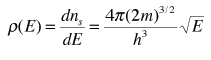
Esto representa el número de estados electrónicos por unidad de volumen por unidad de energía, con energía E. Esta densidad de energía, es un factor en muchas de las propiedades eléctricas de los sólidos. Nótese que el resultado es independiente de la dimensión L, que fue elegida anteriormente, demostrando que la expresión se puede aplicar al material a cualquier escala.