Mostrar Todas las 26 Distribuciones Clásicas

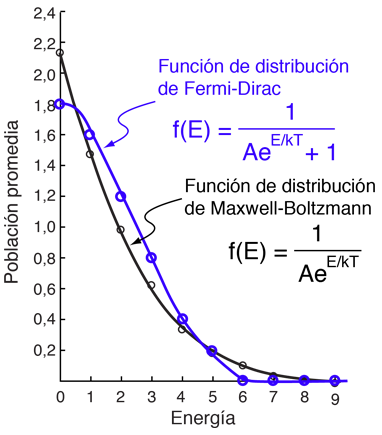
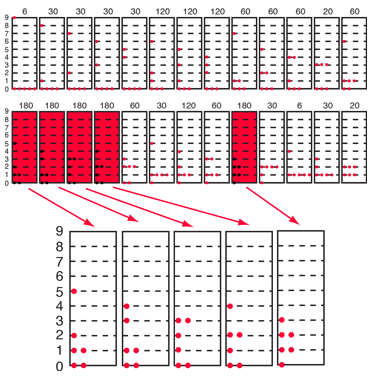
¿De cuantas maneras se pueden distribuir 9 unidades de energía, entre 6 fermiones idénticos e indistinguibles? La estadística de Fermi-Dirac difiere radicalmente de la clásica estadística de Maxwell-Boltzmann, en que los fermiones deben obedecer el principio de exclusión de Pauli. Considerando en este ejemplo que las partículas son electrones, un máximo de dos partículas pueden ocupar cada estado espacial, ya que hay dos estados de espín para cada uno. Aunque había 26 posibles configuraciones para cada partícula distinguible, estas quedan reducidas a 5 estados que tienen no más de dos partículas en cada estado.

La evaluación de la ocupación promedio de cada estado de energía, es mucho más simple que en el ejemplo de Maxwell-Boltzmann, puesto que cada macroestado tiene un peso de 1. El promedio de ocupación es exactamente la suma del número de partículas en un estado de energía dado, sobre todas las 5 distribuciones, dividido por 5.

La Distribución Promedio de 9 Unidades de Energía entre 6 Partículas Idénticas

E Número Promedio Maxwell- Boltzmann Número Promedio Bose- Einstein Número Promedio Fermi- Dirac 0 2,143 2,269 1,8 1 1,484 1,538 1,6 2 0,989 0,885 1,2 3 0,629 0,538 0,8 4 0,378 0,269 0,4 5 0,210 0,192 0,2 6 0,105 0,115 0 7 0,045 0,077 0 8 0,015 0,038 0 9 0,003 0,038 0

Para los fermiones, sólo hay 5 distribuciones posibles de 9 unidades de energía entre 6 partículas, en comparación con 26 distribuciones posibles de partículas clásicas. Para obtener una función de distribución del número de partículas como función de la energía, se debe tomar la población media de cada estado de energía. Arriba se muestra el promedio para cada uno de los 9 estados, en comparación con los resultados obtenidos por la estadística de Maxwell-Boltzmann y la estadística de Bose-Einstein.

Los estados de baja energía son menos probables con las estadísticas de Fermi-Dirac que con la estadística de Maxwell-Boltzmann, mientras que para la gama media de energías son más probables. Aunque esa diferencia no es grande en este ejemplo de un pequeño número de partículas, se hace muy espectacular con números grandes y bajas temperaturas. En el cero absoluto, todos los posibles estados de energía hasta un nivel denominado la energía de Fermi están ocupados, y todos los niveles por encima de la energía de Fermi están vacantes.