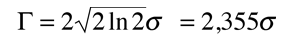Función de Distribución Gausiana
| Distribución | Forma Funcional | Media | Desviación Típica |
| Gausiana | 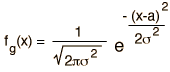 | 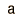 | 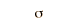 |
Si el número de eventos es muy grande, entonces se puede utilizar la función de distribución de Gauss para describir los fenómenos físicos. La distribución de Gauss es una función continua que se aproxima a la exacta distribución binomial de eventos.
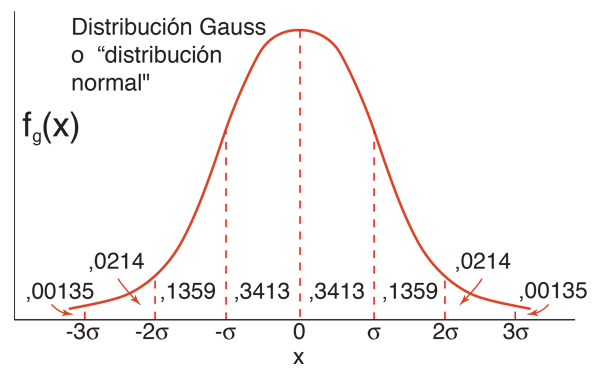
La distribución gausiana mostrada está normalizada, de modo que la suma sobre todos los valores de x da una probabilidad de 1. La naturaleza de la distribución gausiana da una probabilidad de 0.683 de estar dentro de una desviación estándar de la media. El valor de la media es a=np donde n es el número de eventos y p la probabilidad para cualquier valor entero de x (esta expresión proviene trasladada de la distribución binomial). La expresión de la desviación estándar, también proviene de la distribución binomial.
A la distribución Gausiana, se le llama usualmente "distribución normal" y tambien se le conoce como "campana de Gauss".
Mostrar Campana de Gauss
Funciones de Distribución
Conceptos de Estadística Aplicada
| HyperPhysics*****HyperMath*****Álgebra | M Olmo R Nave |