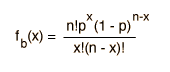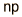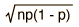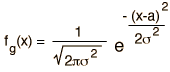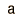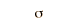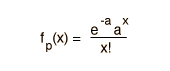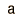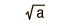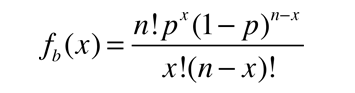Comparación de Funciones de Distribución

Distribución	Forma Funcional	Media	Desviación Típica
Binomial
Gausiana
Poisson

Función de Distribución Binomial

Distribución	Forma Funcional	Media	Desviación Típica
Binomial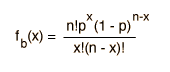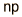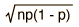

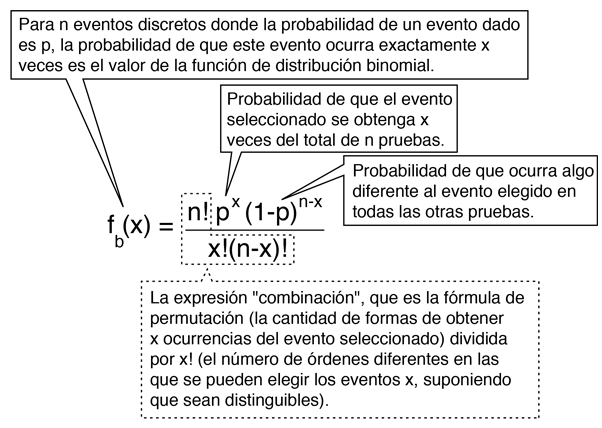
La función de distribución binomial especifica el número de veces (x) que puede ocurrir un evento en un número independiente de tiradas n y donde p es la probabilidad de la ocurrencia del evento en una simple tirada. Es una distribución de probabilidad exacta para cualquier número de intentos. Si n es muy grande se puede tratar como una función continua. Esto es lo que hace la distribución gausiana. Si la probabilidad p es pequeña de modo que la función solo tenga valores significativos para valores pequeños de x, entonces la función se puede aproximar por medio de la distribución de Poisson.

Con los parámetros arriba definidos, las condiciones para la validez de la distribución binomial son

• cada tirada puede dar lugar a uno de dos resultados posibles, lo que podría calificarse de "éxito" o "fracaso".
• la probabilidad de "éxito", p, es constante de una tirada a otra.
• las tiradas son independientes.

Comentarios sobre la Función de Distribución Binomial

Cuando examine la forma de la función de distribución binomial:

Es una colección bastante formidable de símbolos y factoriales. Estos términos surgen del exámen de la probabilidad de eventos discretos. Tal vez el siguiente resumen será útil: