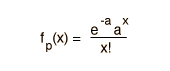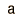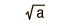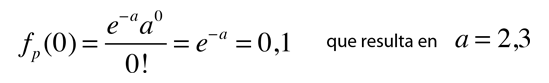Función de Distribución de Poisson

Distribución	Forma Funcional	Media	Desviación Típica
Poisson

Si la probabilidad de p es tan pequeña, de forma que la función solamente es significativa para valores pequeños de x, entonces la distribución de eventos se puede aproximar mediante la distribución de Poisson. Bajo estas condiciones, resulta una aproximación razonable de la distribución binomial exacta de eventos.

En el cálculo de la función de distribución, los valores de la media y desviación estándar se realizan a través de la distribución binomial. En las condiciones en las se aplica la distribución de Poisson, la desviación típica se puede aproximar por la raíz cuadrada de la media.

Intervalos de Confianza

La distribución de Poisson nos proporciona una forma útil para evaluar el porcentaje de tiempo en el que se espera un determinado rango de resultados. Después de hacer una serie de observaciones, es posible que deseemos proyectar un límite superior razonable sobre algún evento.

Por ejemplo, si hemos obtenido un cierto tipo de evento especial solamente una vez (x=1), durante nuestro tiempo de investigación en un gran acelerador después de observar n eventos, podríamos desear proyectar cuantos eventos adicionales tendríamos que observar para tener un 90 % de nivel de confianza en observar al menos una vez tal evento especial. (¡Esto nos podría ayudar a defender, nuestra petición de mas tiempo en el acelerador para la próxima vez!). Esta clase de proyección le viene bien a la estadística de Poisson. Una forma conveniente es calcular el valor medio "a", para el cual el valor de observación de x=0 tiene una probabilidad del 10%. En términos de la distribución de Poisson, esta condición se puede expresar como

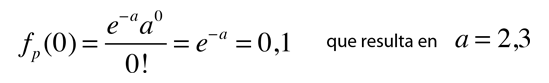
Ahora, puesto que el valor medio es a = n'p, y la probabilidad p = 1/n, donde n es el número de observaciones previas (cuantas observaciones hicimos cuando obtuvimos el evento especial), se sigue que para alcanzar el 90% de nivel de confianza de ver el evento especial otra vez, tendríamos que observar n' = 2,3n eventos mas. Es decir, debemos observar 2,3 veces los eventos que observamos la primera vez, para tener un 90% de nivel de confianza en observar otro evento especial.

Otra forma de interpretar este resultado es que si observamos n eventos sin ver ninguna vez el avento especial deseado, entonces con un 90% de confianza podemos decir que el valor medio de la observación de tal evento es menor de 2,3 = a, donde a = np es el valor medio estándar. Basado en un pequeño número de observaciones de eventos que se presume que actúan por pura probabilidad, podemos hacer una proyección sobre la banda superior para tales eventos al nivel de confianza elegido.