Ejemplo de la Distribución de Poisson

Distribución	Forma Funcional	Media	Desviación Típica
Poisson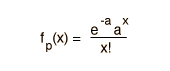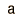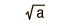

Si la probabilidad de p es tan pequeña, de forma que la función solamente es significativa para valores pequeños de x, entonces la distribución de eventos se puede aproximar mediante la distribución de Poisson. Bajo estas condiciones, resulta una aproximación razonable de la distribución binomial exacta de eventos.

En el cálculo de la función de distribución, los valores de la media y desviación estándar se realizan a través de la distribución binomial. En las condiciones en las se aplica la distribución de Poisson, la desviación típica se puede aproximar por la raíz cuadrada de la media.

La ecuación de Poisson se puede usar en el diseño de experimentos como el de dispersión, donde solo se dan un pequeño número de eventos. Por ejemplo si se conoce el valor promedio que resulta de un experimento estándar, se pueden realizar predicciones sobre futuros resultados.

Supongamos que hemos realizado tres veces un determinado experimento en un acelerador para detectar partículas raras. La primera vez se obtuvo 1, la segunda 5 y la tercera 3.
a. ¿Cuantas ejecuciones deberemos realizar para obtener un total de 100 partículas.?
b. ¿Cuantas ejecuciones deberemos realizar para obtener al menos 5 con un 90% de fiabilidad?

a. Puesto que el número medio de eventos es 3, se espera obtener 100 eventos en 100/3 o 34 ejecuciones. Esta es una proyección razonable, pero no dice nada sobre el nivel de confianza.

b. Deberiamos esperar que con dos ejecuciones, tendríamos suficiente para observar 5 eventos, puesto que la media es 3. Pero las estadísticas de Poisson, nos permite proyectar niveles de confianza. En este cálculo se aborda el problema de manera "hacia atrás", calculando la probabilidad de observar 0, 1, 2, etc. eventos y luego sustrayéndolo de 1, para obtener la probabilidad de ver otros eventos distintos a ese número. Explorando el cálculo obtenido con las entradas de abajo, podemos reunir los números en la siguiente tabla:

La probabilidad de obtener al menos 5 eventos en 2 ejecuciones, debería ser evaluada como la probabilidad de obtener al menos 3 en una ejecuación (0,5768) por la probabilidad de obtener al menos 2 en la otra ejecuación (0,8008) que daría solamente 0,46 o 46% de confianza en dos ejecuaciones. En tres ejecuaciones la probabilidad aumento a (0,8008)(0,8008)(0,9502) = 61%. En 4 ejecuciones 69%, 5 ejecuciones 77%.