Ejemplo de Distribución Binomial

Distribución	Forma de Función	Media	Desviación Típica
Binomial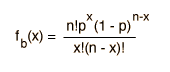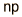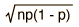

Joe lanza un dado seis veces y saca un tres dos veces. ¿Tiene mucha suerte o es inusual?

La probabilidad básica de sacar un "3" en un tirada es p=1/6 . Luego para n=6 tiradas, el número promedio de salir el 3, sería

De modo que sacar dos veces el número 3, no es definitivamente el resultados esperado o mas probable, pero queda por ver hasta qué punto la probabilidad es menor en relación con el resultado más probable.

Ahora, el número de formas de seleccionar r objetos de un total de n es

que se llama permutaciones de r objetos tomados de un total de n objetos. Si el tomar los mismos objetos o resultados, pero en ordenes diferentes no se consideran que sean resultados diferentes, entonces tenemos que dividir todo por el número de maneras diferentes de disponer los objetos escogidos, que es r!. Entonces, el número de conjuntos distintos que podremos tomar será pues

que se llama combinación de r objetos tomados de un conjunto de n objetos. (Tambien se llama combinación de n objetos tomados de r en r).

La probabilidad de sacar cierto resultado r veces es su probabilidad p^r, pero si haces eso Y obtiene cualquier otro resultado para el resto de las tiradas (probabilidad asociada (1-p)^n-r), entonces la probabilidad de que suceda este resultado combinado es el producto de estas probabilidades. Esto es parte de la naturaleza de la probabilidad general: la probabilidad de que sucedan cualquiera dos resultados relacionados por una lógica "Y", será el producto de las probabilidades de los resultados simples. Entonces, si la probabilidad combinada se multiplica por el número de maneras de obtener este resultado, este producto será pues la función de distribución binomial.

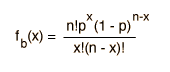
Usando esta función para evaluar la probabilidad de sacar 0,1,2 y 3 veces el "3", tirando el dado seis veces nos da