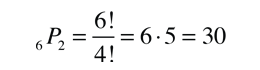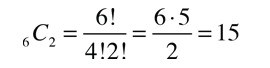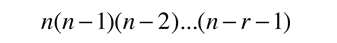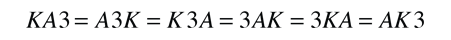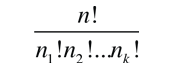Permutaciones
La fórmula de la permutación nos da el número de maneras en que podemos elegir r objetos o eventos, tomados de una colección de n objetos o eventos.

Como en toda la probabilidad básica, las fórmulas nacen del conteo del número de maneras en que pueden suceder cosas específicas, y comparándola con el número total de posibilidades. Si estamos haciendo elecciones de un conjunto de n objetos, entonces en la primera pasada tenemos n elecciones. En la segunda tendremos n-1 elecciones, n-2 en la tercera y así sucesivamente. Como se ilustró antes para 5 objetos, el número de maneras en que podemos tomar los 5 objetos es 5!.
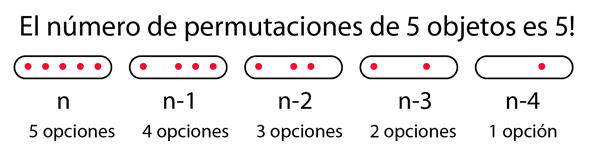
Ahora, si vamos a tomar un subconjunto r del total del número de objetos n, como tomar 5 cartas de una baraja de 52, entonces el proceso de conteo, nos tiene que decir el número de formas diferentes que podemos realizarlo. En la primera pasada tendremos n elecciones, luego n-1 y asi hacia abajo hasta llegar a n-r+1 en la última pasada. Entonces, el número de formas diferentes que podemos hacer esto es
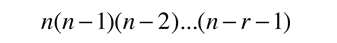
que se puede expresar en la forma estándar

A veces lo que se necesita es el número de permutaciones de r objetos tomados de n, pero tiene el inconveniente de sobreconteo, si lo que necesitamos es obtener el numero de colecciones distintas de objetos o eventos. En un juego de cartas, estas colecciones de tomar estas tres cartas son equivalentes:
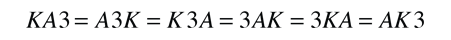
De modo que la fórmula de la permutación cuenta de mas el número de maneras en que podemos obtener esta combinación, si no queremos hacer distinciones en el orden de elección de los objetos. En este caso el factor de sobreconteo es 6 = 3!, el número de permutaciones de 3 objetos. Por lo tanto, el número de colecciones distintas de r objetos, tomados de un conjunto de n objetos, se obtiene dividiendo la fórmula de la permutación por r!. Se escribe normalmente

Para un grupo de n objetos o eventos que están divididos en k subconjuntos, se generaliza la fórmula de arriba para dar el número de permutaciones distintas de los n objetos.
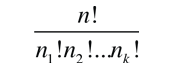
Aquí, los términos del denominador son las poblaciones de los subconjuntos k. Una aplicación de esta fórmula, se encuentra en la determinación del número de posibles estados de energía en una distribución de energía de partículas distinguibles.
|