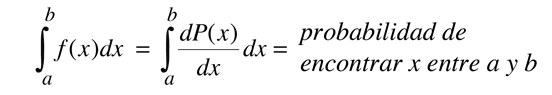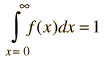Probabilidad Básica
La probabilidad para un determinado evento puede considerarse como, el cociente entre el número de maneras en que puede ocurrir el evento, dividido por el número de maneras en que puede suceder cualquier posible resultado. Si identificamos el conjunto de todos los resultados posibles como el "espacio muestra" S, y al evento deseado lo denotamos por E, entonces la probabilidad del evento E se puede escribir
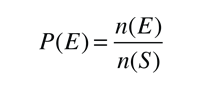
En el lanzamiento de un par de dados, apueste sobre el número 7 porque es el más probable. Hay 6 maneras de obtener un total de 7, de las 36 maneras distintas en que pueden salir los dos dados en un lanzamiento. La probabilidad es entonces
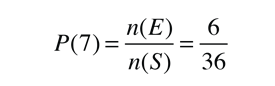
La idea de un "evento" es algo muy general. Supongamos que toma cinco cartas de una baraja estándar de 52 cartas y desea calcular la probabilidad de que las 5 cartas sean corazones. Este evento deseado nos trae la idea de una combinación. El número de maneras en que podemos escoger cinco corazones, sin tener en cuenta que cartas la forman, ni en qué orden, nos lo da la combinación
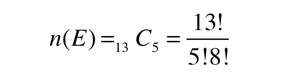
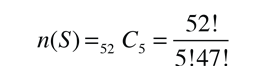
Usamos pues, la misma expresión básica de la probabiliad que en este caso da

Por lo que sacar de una mano cinco cartas del mismo palo, es un evento raro, con una probabilidad de uno entre 2000.
Si deseamos calcular la probabilidad de que ocurran cualquier de n elementos inconexos, tenemos que sumar las probabilidades individuales de cada uno de esos elementos. Por ejemplo, la probabilidad de sacar 5 cartas iguales de cualquier palo, es la suma de 4 probabilidades iguales de sacar las 5 cartas del ejemplo anterior. En lenguaje de lógica, si los elementos están relacionados por el operador lógico "OR", las probabilidades se suman.
Si los eventos está relacionados por el operador lógico "AND", la probabilidad resultante es el producto de las probabilidades individuales. Si queremos obtener la probabilidad de sacar un 7 con dos dados en una tirada y luego volver a sacar otro 7 en la segunda tirada, entonces la probabilidad, será el producto

La expresión de la probabilidad debe ser tal, que la suma de probabilidades para todos los eventos posibles debe ser 1. La restricción de la suma de todas las probabilidades a 1, se llama "normalización". Cuando se calcula la probabilidad mediante el proceso de contar, entonces las probabilidades se obtienen siempre normalizadas. Pero cuando desarrollamos expresiones de probabilidad de eventos en la naturaleza, debemos asegurarnos de que la expresión esté normalizada.
| La Función de Distribución de Probabilidad |
Conceptos sobre Estadística
| HyperPhysics*****HyperMath | M Olmo R Nave |