Trayectoria Vertical
Los objetos moviéndose a altas velocidades a traves del aire encuentran un arrastre del aire proporcional al cuadrado de la velocidad. La descripción del movimiento de objetos bajo este arrastre cuadrático requiere normalmente de técnicas numéricas mas que de una fórmula analítica directa puesto que la fuerza de arrastre y la fuerza gravitacional no actuan a lo largo de la misma línea. En el caso de trayectoria vertical, puede tratarse analíticamente, puesto que esas fuerzas son colineales. Es común expresar la velocidad y el tiempo en términos de la velocidad final vt y el tiempo característico t.
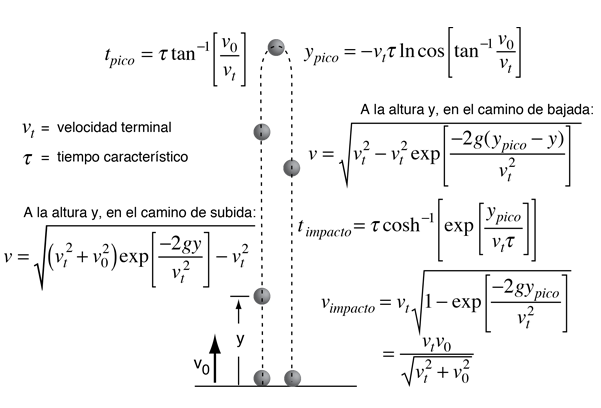
Dos acercamientos comunes a la fuerza de arrastre cuadrática son:
1. Expresar el arrastre en términos de un simple coeficiente de arrastre c: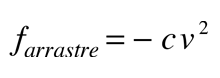
| 2. Asumir que el arrastre es proporcional al area de sección transversal y expresarlo en términos de área y coeficiente de arrastre dependiente de la forma C: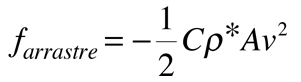
|
Fricción en Fluidos
| HyperPhysics*****Mecánica*****Fluidos | M Olmo R Nave |