Parámetro de Impacto en la Dispersión Nuclear

En la dispersión bajo la influencia de la fuerza de Coulomb, el ángulo de dispersión se relaciona con el parámetro de impacto b, como se ilustra a la izquierda. Bajo el supuesto de que el retroceso del objetivo es despreciable, el cambio en el momento asociado con la dispersión es 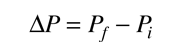donde las magnitudes de los momentos inicial y final son iguales.

La geometría de la dispersión da

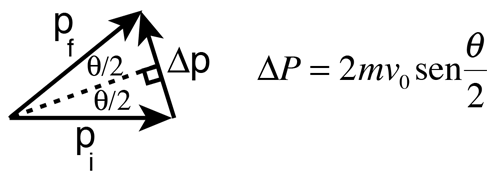
Una forma de obtener una expresión para el cambio en el momento, es usar el concepto de impulso de fuerza, y la simetría de la geometría de dispersión. Solamente la componente del impulso a lo largo del eje de simetría, producirá un cambio de momento neto. De esta forma

Esto da

La conservación del momento angular, se puede utilizar como ayuda en la evaluación de la integral de impulso.

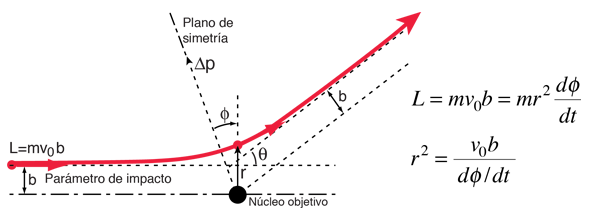
Aquí hemos utilizado la expresión del momento angular de una partícula, y el hecho de que puede ser expresado como el producto de la masa, el radio y la velocidad perpendicular al radio, en cualquier punto de la trayectoria hiperbólica. Sustituyendo da

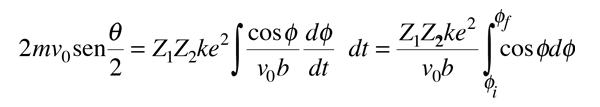
Extendiendo la entrada y salida de la trayectoria de dispersión al infinito, da los límites del ángulo:

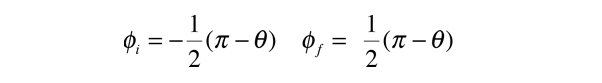
Usando la identidad de la diferencia de ángulo, se pone la integral en la forma

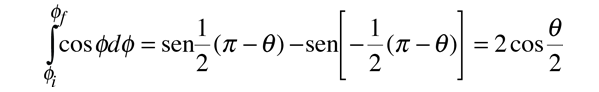
Resolviendo para el parámetro de impacto b, da

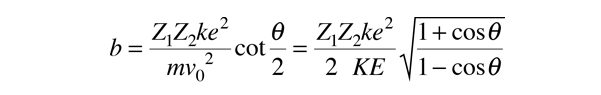
Las dos formas anteriores se puede demostrar que son equivalentes, utilizando las identidades del ángulo mitad. En esta expresión, k es la constante de Coulomb, e la carga del electrón y KE es la energía cinética de la partícula proyectil.