La Paradoja del Remache y el Bicho

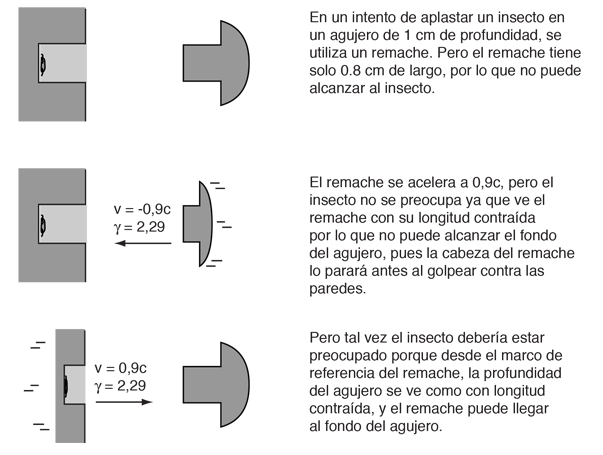
La paradoja del remache y el bicho es una variante de la paradoja de los gemelos, y es similar a la paradoja de la pértiga y el granero, en la que deben abordarse las ideas de simultaneidad en la relatividad. El hecho de que dos eventos sean simultáneos en un sistema de referencia, no implica que sean simultáneos vistos por un observador en movimiento, a una velocidad relativista con respecto a dicho marco.

Para calcular los tiempos de los dos marcos de referencias, considérese el remache entrando en el agujero y hacer t=t'=0 en ese instante y x=x'=0 para establecer el sistema de coordenadas. En los eventos descritos abajo, x' y t' se refieren al marco del remache, mientras que x y t se refieren al marco del bicho. Se usan el factor de relatividad γ = 2,29 y la transformación de Lorentz para transformar cantidades de un marco a otro.

El remache se considera el marco de referencia, y x' y t' se usan para las posiciones y los tiempos.

Transformación de tiempos al marco de referencia del agujero:

Extremo del remache entra en el agujero: t = 0 Cabeza del remache golpea la pared: t = γ(t'+vx'/c2) = 2,29(29,63 ps + (-0,9c)(0,8 cm)/c2) = 12,9 ps Tiempo de llegada del remache al fondo del agujero: t = 2,29(16,14 ps) = 37,04 ps

El bicho no está de acuerdo con este análisis, y encuentra que el tiempo para que la cabeza del remache golpee la pared es anterior al tiempo para que el extremo del remache llegue al fondo del agujero. La paradoja no está resuelta.

Transformando los tiempos medidos en el marco de referencia del bicho al marco de referencia del remache:

Tiempo de impacto de la cabeza del remache t' = γ(12,9 ps) = 29,63 ps El extremo del remache en el marco del bicho está simultáneamente en x=-0,35 cm, pero no es simultáneo con el marco del remache. Transformando da t' =γ(12,9 ps - 0,9c(0,0035)/c2) = 5,63 ps. Si se trata de encontrar un tiempo en el marco del remache cuando el extremo de éste golpea el fondo del agujero, x = -1 cm, t' =γ(37,04 ps - 0,9c(0,01)/c2) = 16,14 ps.

La transformación de tiempos desde el marco de referencia del bicho al marco del remache, da un tiempo para que el extremo llegue -0,35 cm, antes que golpee la cabeza del remache, e incluso sugiere que llega al fondo del agujero antes de que golpee la cabeza del remache. La paradoja no está resuelta.