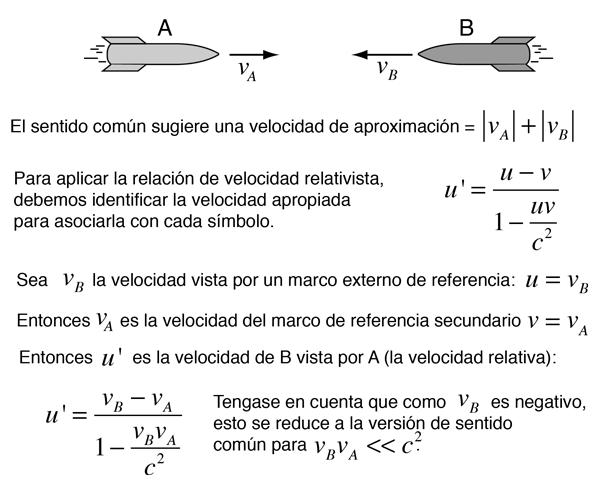
Suma de Velocidades de Einstein

La fórmula de velocidad de Einstein transforma una velocidad medida en un sistema de referencia inercial (u) a una velocidad medida en un marco de referencia (u') que se mueve a velocidad v con respecto de u. En los problemas que implican más de dos objetos, la principal dificultad es la asignación de la velocidad a todos los objetos.

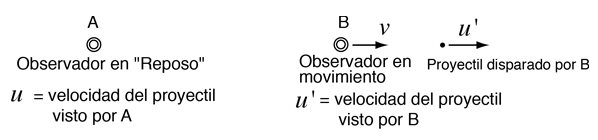
Si A ve B moviéndose a velocidad v, entonces, la velocidad medida por B (u') debería ser vista por A como:

Estas relaciones tienen un sentido perfecto a bajas velocidades, donde ambos denominadores se acercan a 1.

Velocidad Relativa Relativista

La velocidad de la luz es el límite de velocidad del universo, por lo que se deduce que ningún observador, verá cualquier otro observador acercarse o alejarse a una velocidad mayor que c. Pero ¿y si los observadores A y B se mueven al mismo tiempo en direcciones opuestas acercándose con velocidades cercanas a c, según son vistos por un observador externo? ¿Cómo medirán A y B sus velocidades relativas?. Este es un ejemplo de adición de velocidades de Einstein. En el cálculo de abajo, se toman como positivas las velocidades hacia la derecha.

Proyectil Relativista

Ahora bien, si una nave espacial dispara un proyectil a la velocidad Vp medida en el marco de referencia de A, entonces, las dos preguntas relevantes son:

1. ¿Qué velocidad de proyectil verá un observador externo?.

2. ¿Qué velocidad de acercamiento verá B?

Este es un ejemplo de la adición de la velocidad de Einstein.

Si

vA

=

c

y

vP

=

c

entonces

u

=

c.

Nótese que para velocidades bajas, esto es una simple suma de las velocidades de la nave de tiro y el proyectil.

Ahora, para calcular la velocidad de acercamiento, según se ve desde la nave objetivo B:

Si

u(arriba)

=

c

y

vB

=

c

entonces

u'

=

c.

Para velocidades bajas, esta expresión obtiene un valor igual a la suma de las magnitudes de las tres velocidades como se indica en el diagrama. La adición de velocidades de Einstein garantiza que la velocidad resultante no exceda de c, ¡aunque las tres velocidades indicadas se acerquen a c!.