Adición de Velocidades de Einstein

La velocidad relativa de dos objetos nunca excede la velocidad de la luz. Aplicando la transformación de Lorentz a las velocidades, se obtienen expresiones de las velocidades relativas, según son vistas por diferentes observadores. Se llaman fórmulas de adición de velocidades de Einstein.

Estructura Atómica Fina

Uno de los grandes éxitos de la teoría cuántica fué la predicción de los niveles de energía del átomo de hidrógeno. Cuando se hicieron intentos para explicar la estructura fina de las líneas espectrales del hidrógeno, se encontró que el desdoblamiento de las líneas eran erróneas en un factor de dos. Se dieron cuenta de que en el cálculo de las frecuencias, debía usarse la dilatación del tiempo relativista, y estos cálculos mostraron que esta corrección relativista, llamada precesión de Thomas, era el factor 2 necesario de acuerdo con el experimento.

Radiación de Cherenkov

Cuando los objetos altamente radiactivos se observan bajo el agua, tales como reactores en "piscina" y en las áreas subacuáticas de almacenamiento y suministro temporales de combustible de los reactores nucleares, se ven que están bañados en una luz intensa azul, llamada radiación de Cherenkov ó Cerenkov. Es causada por las partículas que entran en el agua, a velocidades superiores a la velocidad de la luz en el agua. Cuando las partículas desaceleran a la velocidad local de la luz, producen un cono de luz aproximadamente análogo, a la ola de proa de un barco que se mueve a través del agua a una velocidad mayor que la velocidad de la ola en la superficie del agua. Otra declaración análoga es, decir que el cono de Cherenkov es como un estampido sónico, excepto que está hecho con luz.

Una de las aplicaciones valiosas de la radiación de Cherenkov está en la detección de neutrinos y la distinción entre los diferentes tipos de neutrinos. Mientras desacelera, un muón energético se mantiene intacto, y su cono de Cherenkov dibuja en la matriz de detectores, un anillo circular bien definido. Por otro lado, un neutrino electrónico de alta energía producirá en los detectores un anillo difuso, porque este neutrino producirá a su vez, una lluvia de electrones, cada uno con su propio cono Cherenkov.

Aplicaciones de Cherenkov

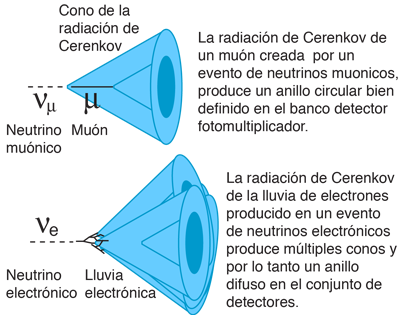
La radiación de Cherenkov se puede utilizar para detectar la aparición de ciertas interacciones nucleares. Estas interacciones pueden liberar grandes cantidades de energía y expulsar partículas a velocidades altamente relativistas. Si estas interacciones tienen lugar en agua u otra sustancia transparente, entonces la radiación de Cherenkov emitida como producto de la reacción viajando a través del agua, puede ser detectada por tubos fotomultiplicadores. Este tipo de detección es el usado en el Observatorio de Neutrinos de Sudbury para detectar las interacciones de neutrinos.

La instalación del detector de neutrinos Super-Kamiokande en Japón, tiene colocado 11.000 tubos fotomultiplicadores para detectar la radiación de Cherenkov, y es capaz de detectar y distinguir los neutrinos electrónicos y los muones.

Las mediciones de las velocidades de las partículas pueden hacerse mediante la medición del ángulo del cono de Cherenkov; es como fotografiar las olas de un buque para medir su velocidad. Una porción de la luz emitida por la partícula desacelerada es coherente y se emite en un ángulo característico

La cantidad total de energía que aparece en la radiación de Cherenkov es pequeña, en comparación con la pérdida total de energía por ionización cuando la partícula entra en el medio. Según Rohlf, una partícula relativista cerca de la velocidad de la luz, pierde energía a razón de aproximadamente 200 MeV/m, y de esa pérdida, sólo alrededor de 40 keV/m será en radiación de Cherenkov, aproximadamente 1/5000 del total.

Aunque el ejemplo dado aquí es para electrones en el agua, que se aplica en la utilización de la radiación de Cherenkov para la detección de neutrinos, la radiación de Cherenkov se produce en cualquier partícula cargada que entre en un medio material, a una velocidad mayor que la velocidad de la luz en ese medio. La radiación de Cherenkov es independiente de la masa de la partícula, dependiendo sólo de su carga y velocidad. Si se produce en un medio ópticamente transparente, la radiación de Cherenkov es emitida en todas las frecuencias en el visible, pero la energía por unidad de longitud de onda es proporcional al inverso del cubo de la longitud de onda. Entonces tienen preferencia las longitudes de ondas cortas, y el color visible lo describe Evans como "blanco azulado".

Los primeros detectores de Cherenkov utilizaban como medios detectores vidrio, lucita y mica. Todos ellos tenían índices de refracción alrededor de n=1,5, por lo que la limitación del ángulo de Cherenkov era aproximadamente 48º. Aunque la radiación de Cherenkov cuando la partícula se ralentiza puede ser producida en todos los ángulos hacia adelante menores que el ángulo limitante, en la práctica la emisión se ve como un cono estrecho con una anchura de solo unos pocos grados. Las partículas desaceleran muy rápidamente, por lo que la radiación proviene de una longitud de recorrido muy corto en el medio, y un intervalo de tiempo muy corto (<10^-10 seg., Richtmyer, et al). La emisión proviene de átomos discretos en las distintas fases a lo largo del camino, y se emite con coherencia. Ya en 1951, Mather informó del uso de la radiación de Cherenkov para determinar una energía de protones de 340 MeV, con una incertidumbre de sólo +/- 0,8 MeV.

Frank & Tam y Fermi llevaron a cabo tratamientos analíticos de la radiación de Cherenkov.

Frecuencia del Ciclotrón

Una de las pruebas iniciales de la expresión de masa relativista fue el comportamiento de los ciclotrones cuando la velocidad de las partículas aceleradas se acercaban a la velocidad de la luz. La expresión no relativista de la frecuencia del ciclotrón, indicaba que las partículas podrían seguir siendo acelerado por una frecuencia angular constante

pero de hecho, eso no se ha demostrado que sea el caso. Se produjeron grandes oscilaciones de carga a altas energías y las partículas no continuaron acelerando. Cuando se incluyó la masa relativista, dando la frecuencia

estuvo claro que la frecuencia debía variar cuando las partículas se aceleraban. El éxito de los aceleradores que utilizaron la frecuencia de arriba, fué una prueba para la expresión de la masa relativista.