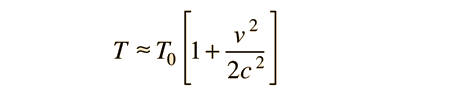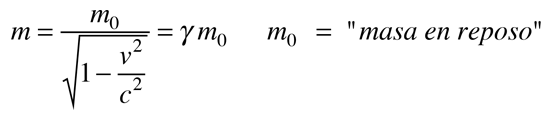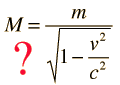Problemas con la Masa Variable
A pesar de que las circunstancias como las del acelerador de Cambridge, están convenientemente descritas asumiendo un aumento de la masa, esta no es la única manera de describir estos experimentos, y hay problemas con el concepto de masa relativista variable. En la siguiente cita se describe el punto de vista de Einstein:
| "No es bueno introducir el concepto de masa de un cuerpo en movimiento, para el cual no se puede dar una definición clara. Es mejor no introducir un concepto de masa distinto que la "masa en reposo" m. En vez de introducir M, es mejor hablar de las expresiones del momento, y la energía de un cuerpo en movimiento." | 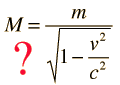 |
Al comenzar el estudio con la relatividad especial por primera vez, es más fácil contemplar conceptos como la velocidad de la luz como el límite de velocidad del universo, imaginando un aumento de la masa hasta el infinito, al alcanzar la velocidad c. Sin embargo, cuando uno se ha familiarizado con los conceptos de momento relativista y energía relativista, no hay necesidad real del concepto de masa variable.
|
Índice
Conceptos de Relatividad |