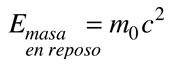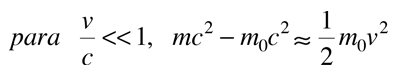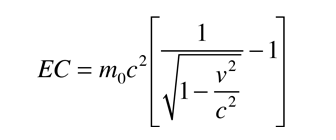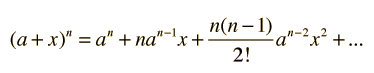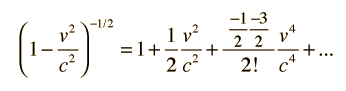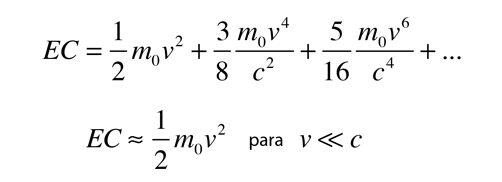Energía Relativista
La famosa ecuación de Einstein de la energía
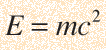
incluye tanto la energía cinética como la energía de la masa en reposo de la partícula. La energía cinética de una partícula de alta velocidad se puede calcular de
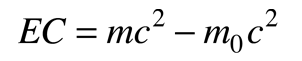
La energía relativista de una partícula, se puede expresar también en términos de su momento en la expresión
 |
|
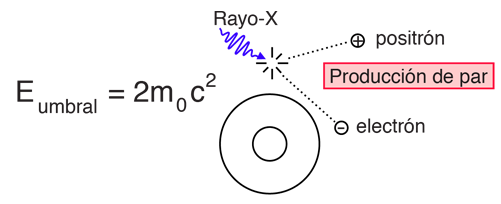
La expresión de la energía relativista es la herramienta utilizada para calcular las energías de enlace del núcleo, y los rendimientos de energía en la fisión y fusión nuclear.
| HyperPhysics*****Relatividad | M Olmo R Nave |