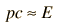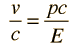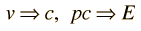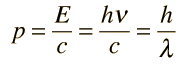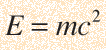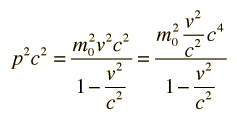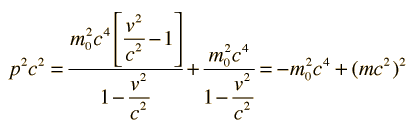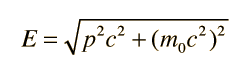Momento Relativista
El momento relativista está dado por

que es la definición ordinarios del momento, pero con la masa sustituida por la masa relativista.
En el cálculo de arriba, una de las formas de expresar la masa y el momento es, en términos de electron voltios. Es típico en la física de alta energía, donde se encuentran las cantidades relativistas, hacer uso de la fórmula de Einstein para relacionar la masa y el momento con la energía. En mecánica relativista, se usa a menudo la cantidad pc en el estudio del momento. Tiene unidades de energía.

Para velocidades relativistas extremas donde  entonces entonces 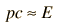 |
Una aplicación útil de la cantidad pc está en el cálculo de la velocidad como fracción de c.
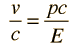 | y cuando | 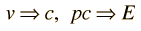 |
con el caso límite, aplicándose al momento del fotón.
|
Índice |


 entonces
entonces