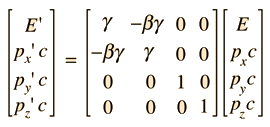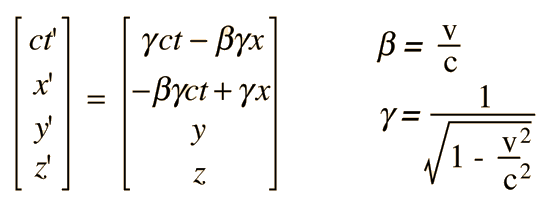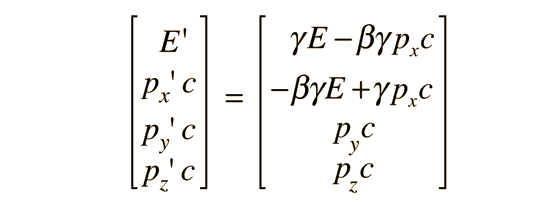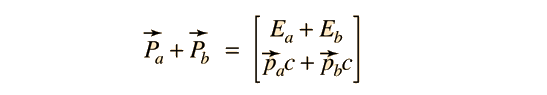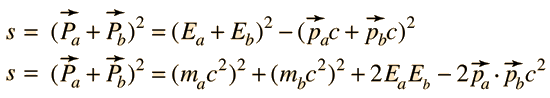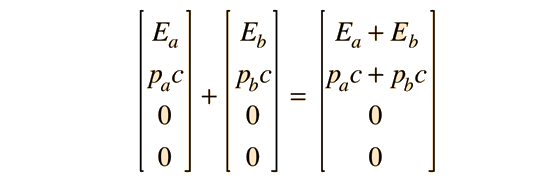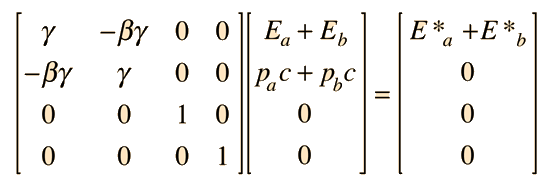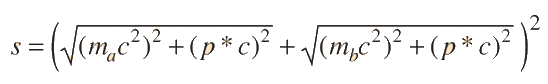Cuadrivectores en Relatividad

En la literatura de la relatividad, las coordenadas del espacio-tiempo y las de la energía/momento de una partícula, se expresan a menudo en forma de cuadrivector (vector de cuatro dimensiones). Se definen de manera que la longitud de un cuadrivector es invariante bajo una transformación de coordenadas. Esta invariancia se asocia con las ideas físicas. La invariancia del cuadrivector de espacio-tiempo, se asocia con el hecho de que la velocidad de la luz es una constante. La invariancia del cuadrivector de la energía-momento, se asocia con el hecho de que la masa en reposo de una partícula es invariante bajo transformaciones de coordenadas.

El cuadrivector de espacio-tiempo se define por	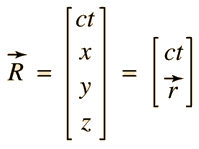El cuadrivector de energía-momento se define por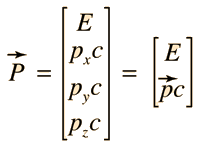
El producto escalar de dos cuadrivectores espacio-tiempo, se define por 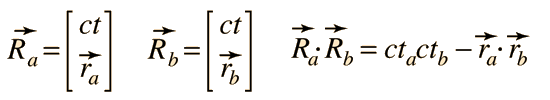El producto escalar de dos cuadrivectores energía-momento, por 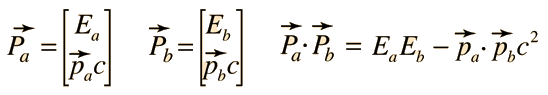Nótese que esto difiere del producto escalar de vectores ordinarios, debido al signo menos. Ese signo menos es necesario para la propiedad de la invariancia de la longitud del cuadrivector.
La longitud del cuadrivector espacio-tiempo al cuadrado está dado por 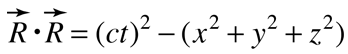La longitud de un cuadrivector es invariante, siendo el mismo en cada sistema inercial. Esta invariancia se asocia con la constancia de la velocidad de la luz. Esta expresión puede ser vista como la ecuación de una esfera, con luz que se propaga desde el origen hacia el exterior a velocidad c en todas las direcciones, de manera que el radio de la esfera en el tiempo t es ct.	La longitud del cuadrivector de energía-momento, está dado por 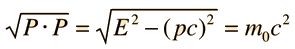La longitud de este cuadrivector es la energía en reposo de la partícula. La invariancia se asocia con el hecho de que la masa en reposo es la misma en cualquier sistema de referencia inercial.

Transformación de Lorentz de Cuadrivectores

La transformación de Lorentz de ambos cuadrivectores de espacio-tiempo y momento-energía, se pueden expresar en forma matricial.

Espacio-Tiempo

Momento-Energía

La transformación de Lorentz del espacio-tiempo, produce el resultado:

y el cuadrivector de energía-momento se transforma en

Suma de Cuadrivectores de Momento-Energía

Dos cuadrivectores de momento-energía, se pueden sumar para formar un cuadrivector.

La longitud de este cuadrivector es invariante

Para el análisis de los momentos de dos partículas en una colisión, se pueden transformar al marco de referencia de momento-cero, lo cual es una ventaja significativa en las colisiones de alta energía. Para las dos partículas, se pueden determinar la longitud del cuadrivector de momento-energía, que es un invariante bajo la transformación de Lorentz. La ventaja práctica de esto en las colisiones de alta energía, es que permite calcular el momento de cada partícula en el marco de referencia de momento-cero. Un enfoque de esto en un sistema de dos partículas, consiste en la adición de los momentos y energías de las dos partículas:

Transformando esto al marco de referencia de momento-cero

Si bien esto da la forma de la transformación necesaria, no sabemos los valores de b y g necesarios para alcanzar la condición de momento-cero. Ahí es donde la invariancia de la longitud del cuadrivector de energía-momento es de valor. Ahora, la evaluación de la longitud del cuadrivector de momento-energía de la información experimental, que tenemos en el marco del laboratorio, da la cantidad s de arriba. Puesto que s se puede evaluar a partir de información de laboratorio, podemos concentrarnos en la expresión de s en el marco de referencia de momento-cero.

donde p*c se ha utilizado para representar el valor de cada momento, ya que están obligados a ser iguales. Esta expresión se puede usar para determinar p*c, y ese valor se puede comparar con el valor original del momento de una de las partículas, para determinar los valores de b y g necesarios para la transformación.