Interacción Fotón-Electrón
Si un fotón de alta energía interactúa con un electrón, la interacción puede ser descrita por la fórmula de dispersión de Compton, o por la formulación del momento relativista de cuadrivectores (vectores de 4 dimensiones). Como un ejemplo específico, considérese un fotón de 10 GeV en una colisión frontal con un electrón en reposo.
Si aplicamos la fórmula de Compton
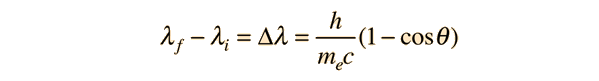
con λ = h/p (relación de deBroglie). Para un fotón retrodispersado donde θ = 180°, esta relación en términos de cantidad pc se convierte en
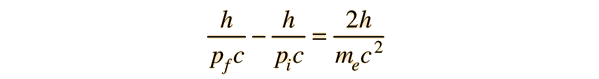
y reordenando da
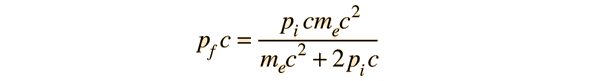
Como pic >> mec2
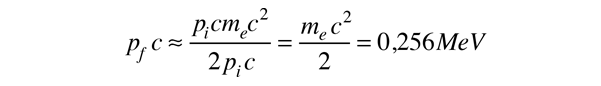
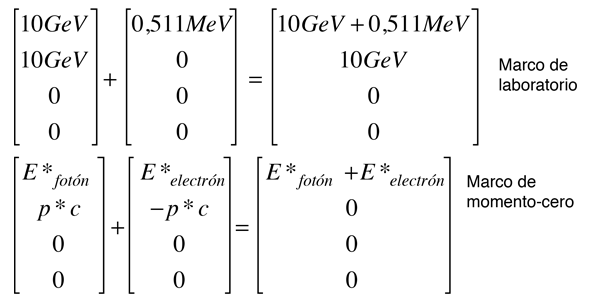
La conservación de la energía nos dice entonces que, la energía del electrón después del choque es 9,999744 GeV. Así que esencialmente toda la energía del fotón es transferida al electrón. Esta situación puede representarse conceptualmente como sigue:

La descripción conceptual que lleva a la conclusión de que el electrón tiene la mayor parte de la energía, después de la conclusión, implica transformar los momentos al marco de referencia de momento-cero, lo cual, disminuye el momento del fotón al tiempo que aumenta el del electrón. Luego en la colisión, se intercambian los momentos en el marco de referencia de momento-cero. A continuación se efectúa la transformación inversa, que reduce aún más la magnitud del momento del fotón, al tiempo que aumenta el momento del electrón. En el ejemplo extremo utilizado aquí, el electrón obtiene la mayor parte de la energía.
La transformación en el marco de referencia de momento-cero sin embargo, no trata de disminuir la energía del fotón a uno de 5 GeV y dar un impulso al electrón de -5GeV/c como se podría esperar. La transformación es mucho más drástica. Se puede llevar a cabo mediante el uso de la energía y del momento como cuadrivectores, y haciendo la transformación de Lorentz necesaria.
La herramienta que se utiliza es la invarianza de la longitud del cuadrivector después de la transformación. Evaluada en el marco del laboratorio, es
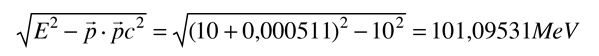
Luego, en el marco de referencia de momento-cero, esta energía se divide entre el fotón y el electrón de tal manera, que sus momentos son iguales en magnitud. Usando la fórmula de energía relativista para expresar la longitud del cuadrivector en términos de los momentos da
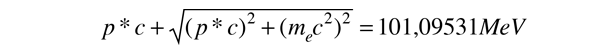
Resolviendo esta ecuación iterativamente da, p*c = 50,5476 MeV. Ahora podemos determinar la velocidad del marco de referencia de momento-cero, determinando la velocidad necesaria para un desplazamiento Doppler del fotón de 10 GeV abajo hasta 50,5476 MeV.
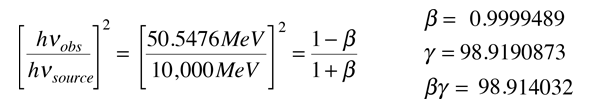
Esto nos permite configurar la transformación de energía/momento
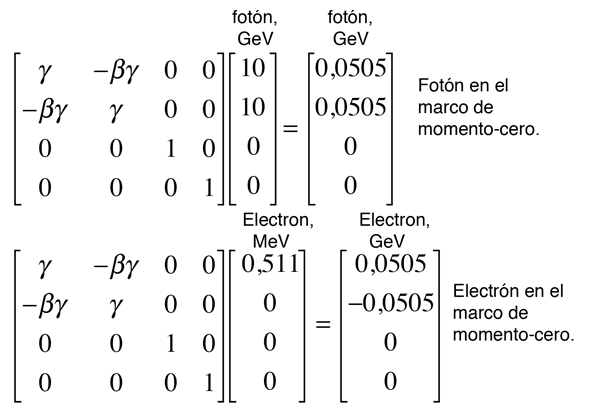
Esta transformación en efecto, nos da un momento cero y conserva la energía. Invirtiendo el signo de β, debe llevarnos de vuelta al marco de referencia del laboratorio.
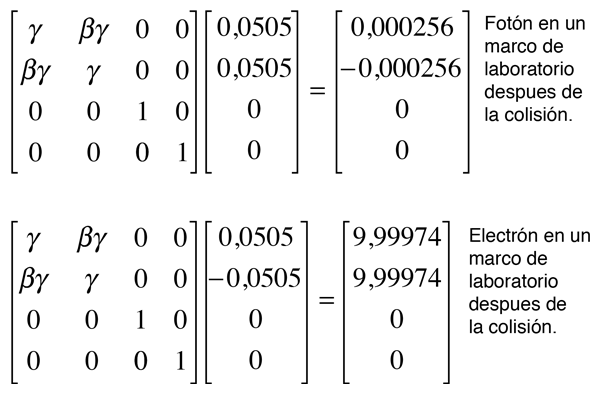
Esta transformación nos da los mismos resultados que se obtuvieron por el método de dispersión de Compton.
| Transformación de Lorentz en forma de Cuadrivector |
| Suma de Cuadrivectores de Momento-Energía |
Referencia
Rohlf
Sec 4-4
| HyperPhysics*****Relatividad | M Olmo R Nave |