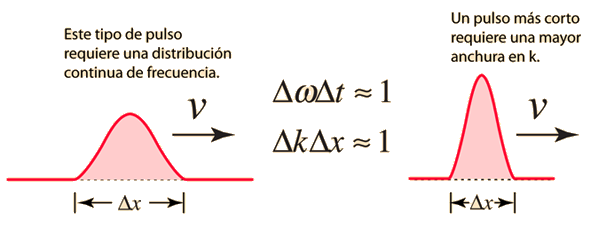
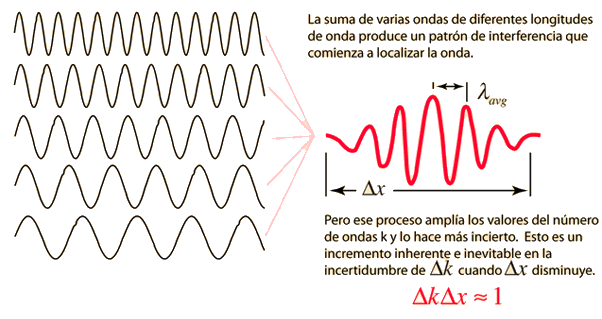
Solución para un Paquete de Ondas

Como la solución de onda de propagación a la ecuación de onda

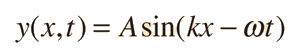
es válida para cualquier valor de los parámetros de onda, y como cualquier superposición de soluciones es también una solución, entonces se puede construir la solución para el paquete de ondas, como la suma de las ondas de propagación:

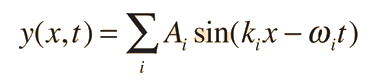
Para un rango continuo de vectores de ondas k, la suma es reemplazada por una integral:

Detalle del Paquete de Ondas

Una solución del paquete de ondas a la ecuación de onda, como un pulso sobre una cuerda, debe contener una gama de frecuencias. Cuanto más corto es el pulso en el tiempo, mayor es la gama de componentes de frecuencia requeridos para el comportamiento transitorio rápido. Este requisito puede ser establecido como una especie de principio de incertidumbre de las ondas clásicas:

Los números reales involucrados dependen de la definición de la anchura del pulso, pero creando pulsos cortos se requiere inherentemente grandes anchos de bandas de frecuencias. Esto es de una naturaleza similar al principio de incertidumbre de la mecánica cuántica.

Paquetes de Ondas de Ondas Discretas

Si se combinan las soluciones de ondas de propagación a la ecuación de onda, se puede utilizar para crear un paquete de onda que empiece a localizar la onda. Esta propiedad de las ondas clásicas se refleja en el principio de incertidumbre de la mecánica cuántica.