El Ensanchamiento de Líneas Espectrales

En el estudio de las transiciones en los espectros atómicos, y de hecho en cualquier tipo de espectroscopia, se debe ser consciente de que las transiciones no son precisamente "nítidas". En las líneas espectrales observadas, hay siempre una anchura finita.

Una fuente del ensanchamiento es el "ancho de línea natural" que surge de la incertidumbre en la energía de los estados involucrados en la transición. Esta fuente de ensanchamiento es importante en espectros nucleares, tales como los espectros Mössbauer, pero rara vez es significativo en espectroscopia atómica. La duración típica de un estado de energía atómica es de aproximadamente 10^-8 segundos, que corresponden a una anchura de línea natural de aproximadamente 6,6 x 10^-8 eV.

En los espectros atómicos en el visible y el ultravioleta, el límite de resolución se fija a menudo por el ensanchamiento Doppler. Con el movimiento térmico de los átomos, aquellos que viajan hacia el detector con una velocidad v, tendrán frecuencias de transición que difieren de las de los átomos en reposo por el desplazamiento Doppler. La distribución de velocidades se puede encontrar a partir de la distribución de Boltzmann.

Puesto que las velocidades térmicas son no relativistas, el desplazamiento Doppler en la frecuencia angular está dada por la forma simple

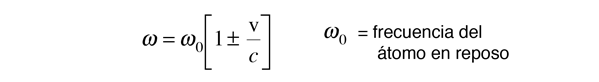
De la distribución de Boltzmann, el número de átomos con velocidad v en la dirección de la luz observada, está dada por

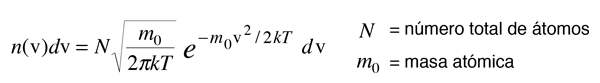
La distribución de la radiación alrededor de la frecuencia central está dada entonces por

Esto es en forma gausiana, el ancho a la mitad del máximo está dado por

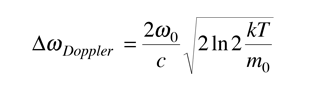
A menudo es conveniente expresar esto en términos de longitud de onda.

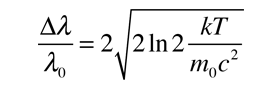
Para los espectros de rotación molecular, cuando se mueve más abajo del espectro, en la región de microondas, el ancho de línea natural surge de nuevo como una mayor fuente de ensanchamiento Doppler. A cierta presión, las perturbaciones de los niveles de energía rotacional por colisiones moleculares (ensanchamiento de presión), se convierte en el factor limitante de la resolución.