Vidas de las Partículas por el Principio de Incertidumbre
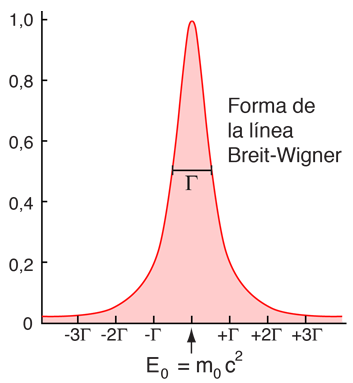 La distribución de Breit-Wigner es similar a la gaussiana cerca del pico, pero las colas de la curva son más planas. |
El principio de incertidumbre es una herramienta para la caracterización de los productos de vida muy corta, producidas en las colisiones de alta energía en los aceleradores. El principio de incertidumbre en la forma
 sugiere que en las partículas con vida extremadamente cortas, habrá una incertidumbre significativa en la energía medida. La medición un gran número de veces, de la energía de masa de una partícula inestable, da una distribución de energías llamada distribución Lorentziana o Breit-Wigner. |
Si se denomina la anchura de esta distribución a mitad del máximo Γ, entonces la incertidumbre en la energía ΔE podría ser razonablemente expresada como
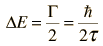
donde se toma el tiempo de vida de la partícula τ, como la incertidumbre del tiempo τ = Δt.
En experimentos de dispersión de alta energía, pueden ser determinadas la incertidumbre de energía ΔE y el tiempo de vida implícita de ella. En otros casos, el tiempo de vida se mide de manera más conveniente, y la "anchura de partícula" en energía implícita, por esa medición.
Γ es referido a menudo como el "ancho de línea natural". Es de gran importancia en la física de alta energía del acelerador, en las que proporciona el medio para determinar los tiempos de vida ultracorta de las partículas producidas. Para la espectroscopia óptica es un factor de menor importancia, debido a que el ancho de línea natural es típicamente 10-7 eV, alrededor de una décima más que el ensanchamiento Doppler. Otra fuente de anchura de línea es el retroceso de la fuente, pero eso es insignificante en el rango óptico.
En transiciones nucleares con emisión gamma en el rango de 0,1-1 MeV, el ancho de retroceso es típicamente mucho mayor que la anchura de línea natural. El retroceso del núcleo emisor, implica que los fotones gamma emitidos, no pueden ser absorbidos por un núcleo idéntico, debido a que su energía es reducida en una cantidad mayor, que la anchura de línea natural de los niveles de absorción potenciales. Mossbauer descubrió que la absorción podría llevarse a cabo, poniendo la fuente sobre un brazo giratorio, para darle la velocidad suficiente para compensar el efecto de retroceso. El efecto Mossbauer, se convirtió en una herramienta experimental útil, cuando se descubrió que el retroceso podría ser suprimido, poniendo el núcleo emisor en una red cristalina. Los gammas emitidos luego, exhibieron algo cercano a la anchura de línea natural, y pudieron ser absorbidos por otros núcleos idénticos.
| Ancho de Línea Natural del Hierro |
| Una Breve Descripción del Tiempo |
Conceptos del Principio de Incertidumbre
Referencia
Rohlf
Cap. 5
| HyperPhysics*****Física Cuántica | M Olmo R Nave |