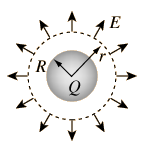
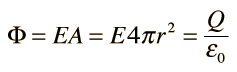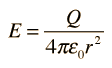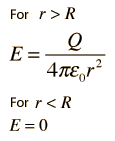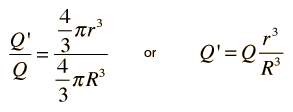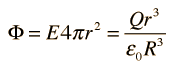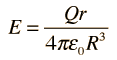Interior de una Esfera Cargada
|
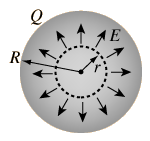
El campo eléctrico interior de una esfera de carga uniforme está dirigido radialmente hacia afuera (por simetría), pero la superficie gausiana esférica, englobará menos de la carga total Q. La carga interior al radio r está dada por la proporción entre volúmenes:
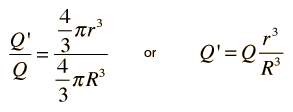
|
| y el campo eléctrico será |
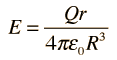 |
Note que el límite en r = R está en concordancia con la expresión para r >= R. La carga esférica simétrica hacia fuera del radio r no afecta al campo eléctrico en r. De lo que se sigue que, en el interior de un cascarón esférico de carga habrá un campo eléctrico cero.
|
Índice
Conceptos sobre Campo Eléctrico |