Lógica Digital
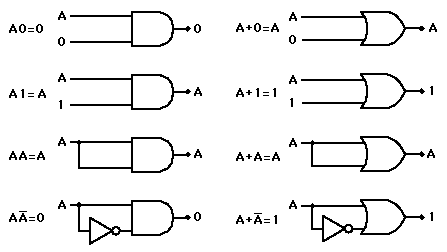
Hay 16 funciones posibles para dos variables binarias (que toman los valores 0 y 1). Estas funciones desarrollan solamente las tres operaciones que conforman el Álgebral de Boole (álgebra booleana): Y, O y Complemento/NOT (NO). Se representan simbólicamente como siguen:
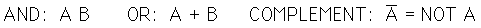
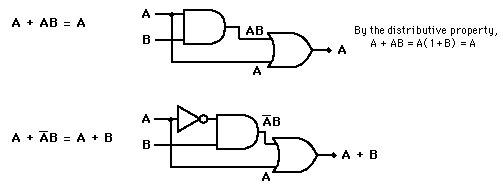
Estas operaciones son como las del álgebra ordinaria, y tienen las propiedades commutativa, asociativa, y distributiva. Hay un grupo de teoremas útiles del álgebra de Boole, que ayudan a desarrollar la lógica para una determinada operación.
| Teoremas Lógicos Digitales | Funciones Lógicas Digitales |
Conceptos de Electrónica
Circuitos Digitales
| HyperPhysics*****Electricidad y Magnetismo | M Olmo R Nave |