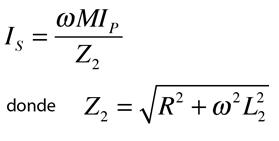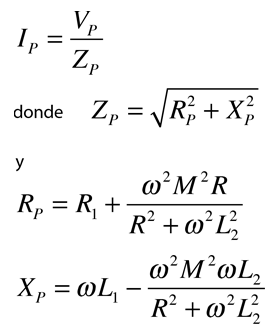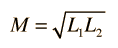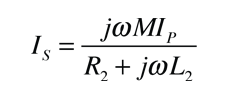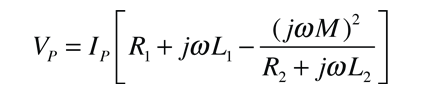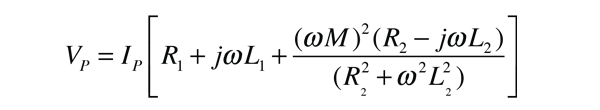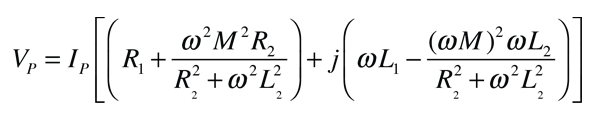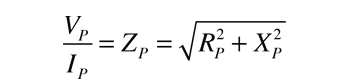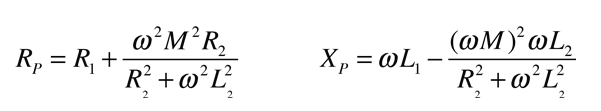Ecuaciones de Circuitos: Transformador

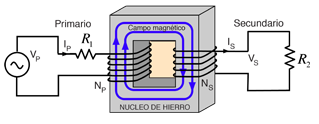
La aplicación de la ley de voltaje a ambos circuitos primario y secundario de un transformador da:

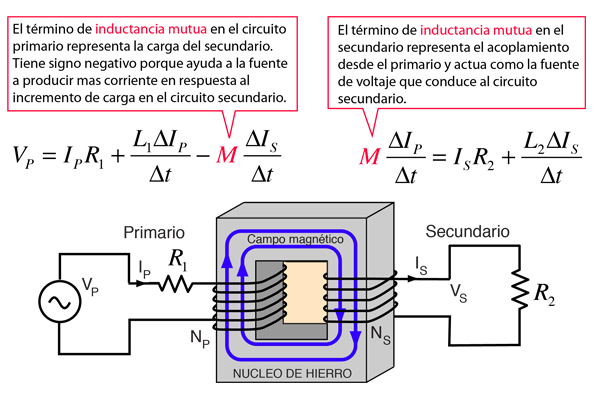
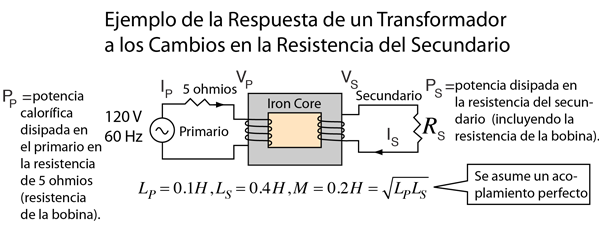
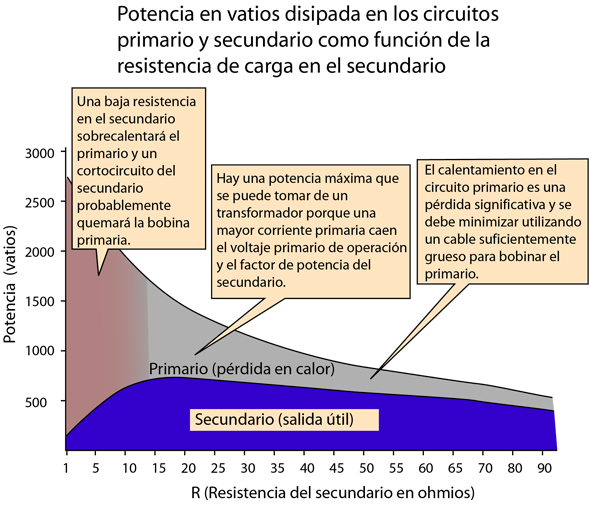
El transformador constituye las más común aplicación del concepto de inductancia mutua. Por efecto de la inductancia mutua del transformador, el circuito primario toma mayor potencia de la alimentación eléctrica en respuesta a un incremento de la carga en el secundario. Por ejemplo, si la resistencia de carga en el secundario se reduce, la potencia requerida aumentará, forzando al lado primario del transformador a suministrar mas corriente para cubrir la necesidad adicional.

Ecuaciones de Circuitos: Transformador

La ecuación del circuito secundario es la de un circuito RC alimentado por una fuente de voltaje: La corriente del circuito primario está dada por: Mostrar

Nota: la impedancia efectiva del circuito primario no contiene solamente la impedancia mutua de acoplamiento, sino que contiene términos dependientes de la resistencia de carga del secundario R. Cuando R es mas pequeño (mayor carga), ZP viene a ser mas pequeña y resistiva, tomando mas potencia de la alimentación del primario. Para un acoplamiento ideal, la inductancia mutua viene a ser

En la operación de un transformador, hay un rango medio práctico de resistencia de carga. En el ejemplo de arriba se puede observar que la máxima potencia de salida, se obtiene con una resistencia de carga de entre 15 y 20 ohmios. Cuando se extrae una carga del secundario demasiado pesada, la bobina primaria se calienta y aumenta el "zumbido" audible del transformador. Mi hermano Edgar Nave, trabajó en una constructora eléctrica comercial y ha cableado muchos transformadores grandes. Informa de incidentes donde el secundario del transformador estaba en cortocircuito y comenta que el transformador "chillaba" igual que una bestia herida, antes de quemarse su bobina primaria.

Ecuaciones de Circuitos: Transformador

La aplicación de la ley de voltaje a ambos circuitos primario y secundario de un transformador da:

Para obtener las ecuaciones del circuito se necesita la solución simultánea de las ecuaciones del circuito primario y secundario. Esa solución se facilita usando el método de impedancia compleja, suponiendo un suministro de voltaje sinusoidal con frecuencia angular ω. En la práctica estandar de CA (corriente alterna) se usan corrientes y voltajes rms, y en el enfoque de la impedancia compleja la derivada de la corriente dI/dt = jωI. Las ecuaciones de los bucles primario y secundario toman entonces la forma:

Desde la ecuación del circuito secundario podemos encontrar una expresión para la corriente secundaria I_S.

Esto se puede sustituir en la ecuación del bucle primario:

El último término se puede racionalizar multiplicando numerador y denominador por

dando

Esto nos permite separar las partes real e imaginaria y colocar la expresión en la forma de un número complejo estándar.

Esto se puede escribir en la forma de impedancia Z de un circuito estándar de AC:

donde