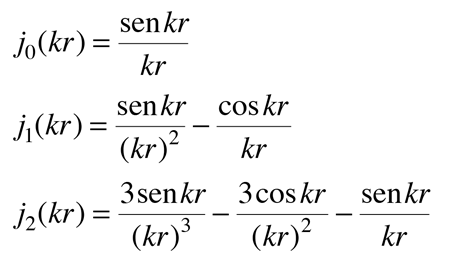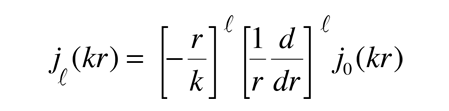Funciones de Bessel

Las funciones de Bessel forman una clase de función de las denominadas funciones especiales que se encuentran en la solución de determinados problemas físicos. Dan la solución a una ecuación diferencial muy importante, la ecuación de Bessel:

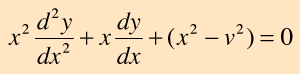
Las soluciones para esta ecuación están en la forma de series infinitas, que se llaman funciones de Bessel de primera especie. La expresión para la suma es

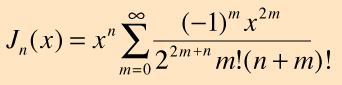
Los valores para las funciones de Bessel se pueden encontrar en la mayoría de las colecciones de tablas matemáticas. Las funciones de Bessel se encuentran en situaciones físicas donde hay simetría cilíndrica. Esto ocurre en problemas relacionados con los campos eléctricos, vibraciones, calor por conducción, la difracción óptica y otros.

Otra forma llamada función de Bessel esférica, aparece en una aplicación específica de mecánica cuántica, el pozo de potencial esférico.

Funciones de Bessel Esféricas

Una clase específica de las funciones especiales llamadas funciones esféricas de Bessel se plantea en los problemas de simetría esférica, como el pozo de potencial esférico en la mecánica cuántica. Las tres primeras formas son

Las formas de ordenes superiores, se pueden generar a partir de la primera forma mediante la relación

A veces es útil contar con los casos límites de estas funciones para distancias muy grandes o muy pequeñas: