Difracción Abertura Circular

Cuando la luz de una fuente puntual pasa a través de una abertura circular pequeña no produce como imagen un punto brillante, sino más bien un disco difuso circular conocido como disco de Airy, rodeado de anillos circulares concéntricos mucho más tenues. Este ejemplo de la difracción es de gran importancia, porque tanto el ojo humano como muchos instrumentos ópticos, tienen aberturas circulares. Si esta deformación de la imagen de la fuente puntual, es mayor que la producida por las aberraciones del sistema, se dice que el proceso de imágenes está limitado por difracción, y que es lo mejor que se puede hacer con ese tamaño de abertura. Esta limitación en la resolución de las imágenes se cuantifica en términos del criterio de Rayleigh, de modo que se puede calcular el límite de resolución de un sistema.

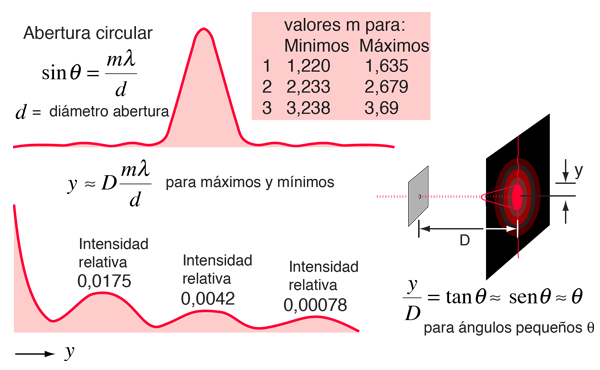
El patrón de difracción de la abertura de arriba fue fotografiado con una película de diapositivas Fuji Sensia 100ASA y luego digitalizado. Con el tiempo de exposición necesario para mostrar los lóbulos laterales, el pico central quedó sobreexpuesto (imagen blanqueada). El único retoque de la imagen digital fue pintar de rojo la parte sobreexpuesta del máximo central (el disco de Airy). El agujero se hizo mediante la colocación de papel de aluminio sobre una placa de vidrio, pegando un alfiler en el papel de aluminio, y luego girando el papel de aluminio. Se hicieron varios agujeros, y este era el más redondo.

Descripción Matemática de la Difracción de Abertura
Ejemplo de Corona alrededor de Gotas de Niebla
Corona alrededor de la Luna
 Índice

Conceptos de Difracción

Difracción de Fraunhofer
 
HyperPhysics*****Luz y VisiónM Olmo R Nave
 Atrás












Difracción Abertura Circular

Para una luz monocromática de longitud de onda λ = nm

incidiendo sobre una abertura circular de diámetro d = micrómetros,

d = x 10^ m,

y proyectado sobre una pantalla a una distancia D = m,

el desplazamiento desde la línea central de la pantalla está dado por la fórmula

Desplazamiento y = distancia pantalla D * valor de m * longitud de onda / diámetro de la abertura

Se puede usar la fórmula activa de arriba para calcular el desplazamiento y, la longitud de onda o el diámetro de la abertura, haciendo clic sobre esas cantidades. Se debe entrar primero los datos conocidos, luego hacer clic sobre la cantidad deseada. Los datos introducidos no se verán forzados a ser consistentes, hasta que se haga clic sobre la cantidad a calcular. El cálculo del desplazamiento y, dará las posiciones de todos los máximos y mínimos de la tabla de abajo. Se puede cambiar cualquier cantidad en la tabla con objeto de calcular los otros parámetros. La fórmula activa de arriba está escrita con la aproximación del ángulo pequeño, pero el cálculo usa la fórmula trigonométrica completa.

Esto produce el siguiente patrón de máximos y mínimos en la intensidad de la difracción

Orden
Mínimo
Máximo
valor m
Desplazamiento y
(cm)
θ
(gradso)
m value
Desplazamiento y
(cm)
θ
(grados)
1
1,220
1,635
2
2,233
2,679
3
3,238
3,69
Cuando la luz de una fuente puntual pasa a través de una abertura circular pequeña no produce como imagen un punto brillante, sino más bien un disco difuso circular conocido como disco de Airy, rodeado de anillos circulares concéntricos mucho más tenues. Este ejemplo de la difracción es de gran importancia, porque tanto el ojo humano como muchos instrumentos ópticos, tienen aberturas circulares. Si esta deformación de la imagen de la fuente puntual, es mayor que la producida por las aberraciones del sistema, se dice que el proceso de imágenes está limitado por difracción, y que es lo mejor que se puede hacer con ese tamaño de abertura. Esta limitación en la resolución de las imágenes se cuantifica en términos del criterio de Rayleigh, de modo que se puede calcular el límite de resolución de un sistema.

Índice

Conceptos de Difracción

Difracción de Fraunhofer

Referencias
Jenkins and White
Sec 15.8

Hecht
Sec 10.2
 
HyperPhysics*****Luz y VisiónM Olmo R Nave
 Atrás