Valores Propios y Funciones Propias

La función de onda de un sistema físico dado, contiene la información medible sobre el sistema. Para obtener los valores específicos de los parámetros físicos, por ejemplo la energía, se opera sobre la función de onda con el operador mecánico cuántico asociado con ese parámetro. El operador asociado con la energía es el hamiltoniano , y la operación sobre la función de onda es la ecuación de Schrödinger. Existen soluciones para la ecuación de Schrodinger independiente del tiempo, solamente para ciertos valores de energía, y estos valores se llaman "Eigenvalores *" de la energía.

Correspondiente a cada valor propio hay una "Eigenfunción *". La solución a la ecuación de Schrödinger para una energía dada 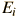, implica también la búsqueda de la función específica 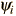que describe dicho estado de energía. La solución de la ecuación de Schrödinger independiente del tiempo toma la forma

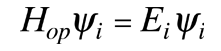
El concepto de valor propio no se limita a la energía. Cuando se aplica a un operador general Q, puede tomar la forma

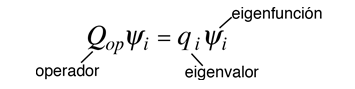
si la función ψ_i es una función propia de ese operador. Los valores propios q_i, deben ser discretos, y en tales casos se puede decir que la variable física está "cuantizada", y que el índice i, hace el papel de "número cuántico" que caracteriza a ese estado.

*"Eigenvalue" viene del alemán "Eigenwert", que significa el valor propio o característico. "Eigenfunciones" es de "Eigenfunktion" significando "función propia o característica".