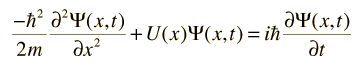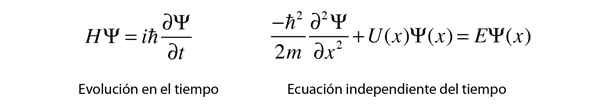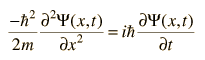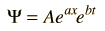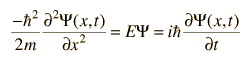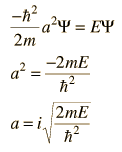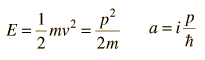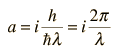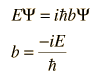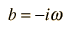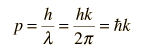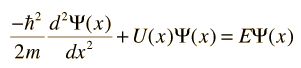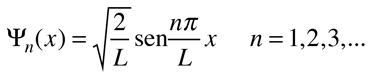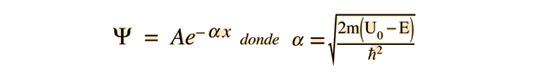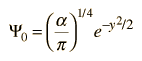Ecuación de Schrodinger Dependiente del Tiempo

La ecuacion de Schrodinger dependiente del tiempo en una dimensión espacial, tiene la forma

Función de Onda de Partícula Libre

En una partícula libre, la ecuación de Schrodinger dependiente del tiempo, toma la forma

y dada la dependencia de tanto la posición como del tiempo, se intenta una función de onda de la forma

Suponiendo que la función de onda representa un estado de energía determinada E, la ecuación puede ser separada por el requisito

Procediendo separadamente con las ecuaciones de posición y de tiempo, y tomando las derivadas indicadas:

Tratando el sistema como una partícula, donde Utilizando ahora la fórmula de De Broglie y la relación de onda:

Tratando el sistema como un paquete de ondas, o una entidad de tipo fotón, donde la hipótesis de Planck da se puede evaluar la constante b

Esto da una solución de onda plana:

Mas Detalles

Onda de Partícula Libre

La función de onda de partícula libre general es de la forma

que como función compleja, se puede expandir en la forma

Fórmula de Euler

Para una aplicación determinada de esta función, podría ser apropiada bien la parte real, o la parte imaginaria. En general, se está interesado en partículas que están libres dentro de alguna clase de contorno, que impone unas condiciones límites fijadas por algún tipo de potencial. El problema de la partícula en una caja, es el ejemplo mas simple.

La función de onda de partícula libre está asociada con un momento conocido con precisión:

pero el requisito para la normalización, hace que la amplitud de la onda tienda a cero, cuando la onda se extiende hasta el infinito (principio de incertidumbre).

Ecuación de Schrödinger Independiente del Tiempo

La ecuación de Schrödinger independiente del tiempo en una dimensión es de la forma

donde U (x) es la energía potencial, y E representa la energía del sistema. Tiene un número importante de aplicaciones físicas en mecánica cuántica. Una parte clave de la aplicación a los problemas físicos es el ajuste de la ecuación a las condiciones físicas de contorno.

Se generaliza fácilmente a tres dimensiones, y se utiliza a menudo con coordenadas polares esféricas.

Valores Propios de Energía

Para obtener valores específicos de energía, se opera sobre la función de onda, con el operador mecánico cuántico asociado con la energía, llamado hamiltoniano. La operación del hamiltoniano sobre la función de onda es la ecuación de Schrodinger. Existen soluciones para la ecuación de Schrödinger independiente del tiempo sólo para ciertos valores de energía y estos valores se denominan "valores propios" de energía.

Por ejemplo, los valores propios de energía del oscilador armónico cuántico están dados por Los estados vibracionales mas bajos de las moléculas diatómicas, se ajustan a menudo con el modelo del oscilador armónico cuántico con la suficiente precisión, para permitir la determinación de las constantes de la fuerza de adherencia de las moléculas.

Mientras que los valores propios de energía pueden ser discretos para pequeños valores, por lo general viene a ser continuo a energías suficientemente altas, porque el sistema ya no puede existir como un estado ligado. Para un potencial de oscilador armónico más realista (representando quizás una molécula diatómica), los autovalores de energía se acercan más y más cuando se aproximan a la energía de disociación. Los niveles de energía después de la disociación, pueden tomar los valores continuos asociados con las partículas libres.

Ecuación de Schrodinger en 1-D

La ecuación de Schrodinger independiente del tiempo, es útil para encontrar valores de energía en sistemas de una dimensión

Comentarios Conceptuales

Esta ecuación es útil para el problema de partícula en una caja que produce:

Para evaluar la penetración de barrera, se calcula la función de onda en el interior de la barrera, que es de la forma:

El oscilador armónico cuántico en una dimensión es:

Esta es la función de onda del estado fundamental, donde y es el desplazamiento desde el equilibrio.

Condiciones de Contorno Físicas y el Teorema de Singularidad

Para las aplicaciones físicas de la mecánica cuántica que implican la solución de la ecuación de Schrodinger como las de la ecuación de Schrodinger independiente del tiempo, uno debe encontrar soluciones matemáticas específicas que se ajusten a las condiciones de contorno físicas del problema.

Una idea muy importante en las ecuaciones diferenciales es el "teoremoa de singularidad", que básicamente dice que si se puede encontrar una solución a la ecuación diferencial que se ajuste a las condiciones físicas de contorno del problema que se está considerando, entonces esa es la solución correcta. Eso lleva a comentarios típicos de los estudiantes sobre ecuaciones diferenciales como "si puedes adivinar la solución y forzarla a ajustarse a las condiciones de contorno, entonces tienes la respuesta correcta."

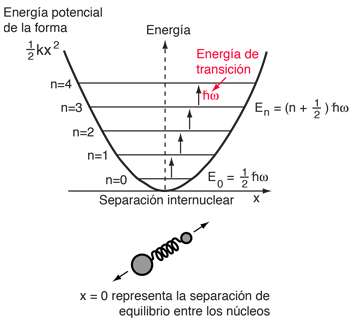
La ecuación de Schrodinger independiente del tiempo se utiliza para una serie de problemas prácticos. Los sistemas con estados ligados están relacionados con la "partícula en una caja" de la mecánica cuántica, la penetración de barrera es importante en el decaimiento radiactivo, y el oscilador mecánico cuántico es aplicable a los modos de vibración molecular.

Si, por ejemplo, vamos a la "partícula en una caja", se encuentra que para una caja de paredes infinitas la función de onda debe ser igual a cero en los bordes de la caja, y se puede proponer una solución de onda sinusoidal y forzarla a encajar las condiciones de contorno. ¿Cómo se sabría proponer una solución de onda sinusoidal? Bueno, en muchas áreas de las matemáticas y las ciencias, "nos apoyamos sobre los hombros de gigantes" y podemos aprovechar el hecho de que muchos en el pasado han explorado este tipo de problemas y pueden sugerirnos los tipos de soluciones que se pueden probar. Esto es parte de la naturaleza de aplicar las ecuaciones diferenciales a problemas físicos.