Enfoque de la Partícula Libre con la Ecuación de Schrodinger
Aunque la ecuación de Schrödinger no puede ser derivada, se puede demostrar que es consistente con los experimentos. La prueba más válida de un modelo es si describe fielmente el mundo real. La naturaleza ondulatoria del electrón, ha sido claramente demostrada como en el experimento de Davisson-Germer y otros. Esto plantea la pregunta de "¿Cuál es la naturaleza de una onda?". Respondemos en retrospectiva, diciendo que la onda es la función de onda del electrón. A partir de la expresión para una onda de propagación en una dimensión, se puede realizar la conexión con la ecuación de Schrödinger. Este proceso hace uso de la fórmula de De Broglie entre la longitud de onda y el momento, y la fórmula de Planck entre la frecuencia y la energía.
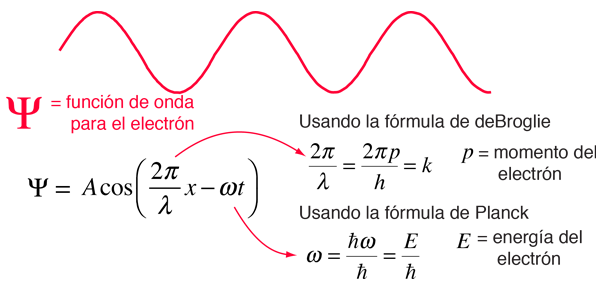
Es más fácil mostrar la relación con la ecuación de Schrodinger, generalizando esta función de onda a una forma exponencial compleja, mediante la fórmula de Euler. Esta es la forma estándar de la función de onda de una partícula libre.
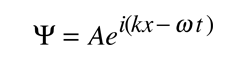
Si ahora se toman las derivadas parciales de esta función de onda con respecto a la posición y el tiempo, se puede demostrar que estas derivadas están relacionadas con el momento y la energía, respectivamente.
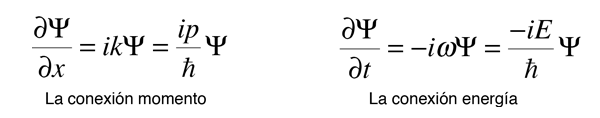
Cuando una operación sobre una función devuelve una constante multiplicada por la función, esa constante se denomina valor propio, y la función es una función propia. Las fórmulas anteriores pueden reordenarse como sigue.
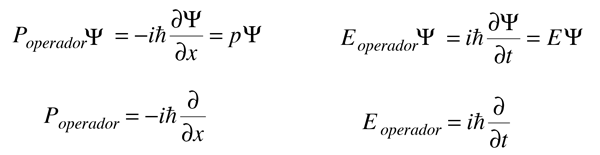
Es costumbre desarrollar los "operadores" de la mecánica cuántica, para los correspondientes observables físicos.
La conexión con la ecuación de Schrödinger puede llevarse a cabo, examinando las expresiones de energía de ondas y partículas:

Aceptando la equivalencia de estas dos expresiones de la energía, y poniéndolas en ambos operadores de la mecánica cuántica, nos lleva a la ecuación de Schrodinger
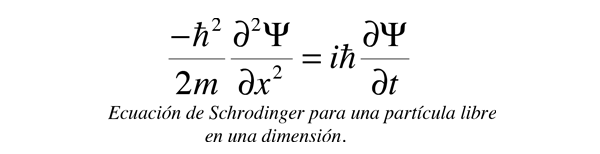
Conceptos de la Ecuación de Schrödinger
| HyperPhysics*****Física Cuántica | M Olmo R Nave |