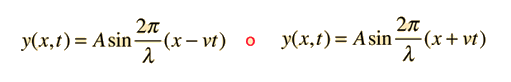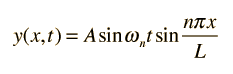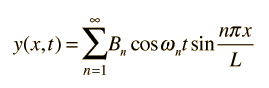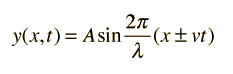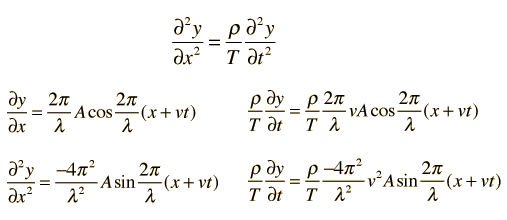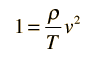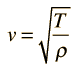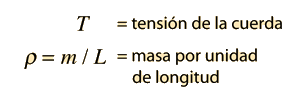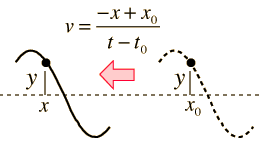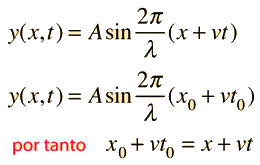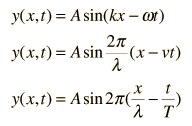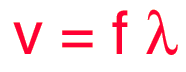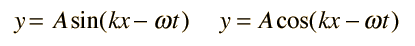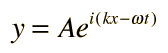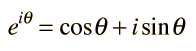Parámetros de Ondas de Propagación
Una solución de onda de propagación a la ecuación de onda se puede escribir de varias maneras diferentes, con diferentes opciones de los parámetros relacionados. Estos incluyen los parámetros de movimientos periódicos básicos de amplitud, período y frecuencia.
Formas equivalentes de la solución de ondas:
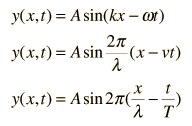
|
Parámetros de onda:
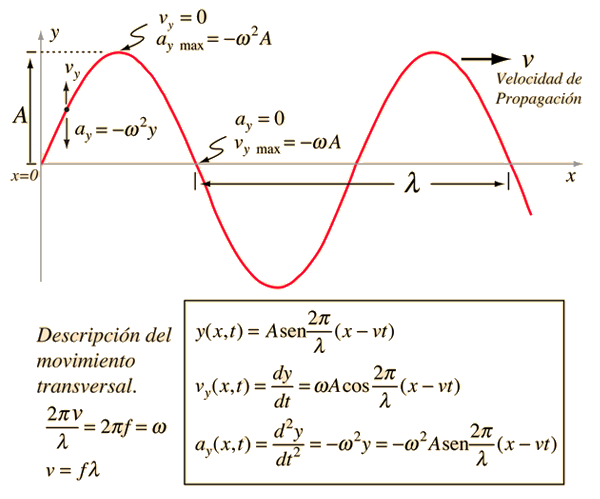
| *Amplitud A
*Periodo T = 1/f
*Frecuencia f = 1/T
*Velocidad de propagación v
|
*Longitud de onda λ
*Número de Onda k = 2π/λ
*Frecuencia Angular ω = 2πf
*Relaciones de onda v = fλ
|
|
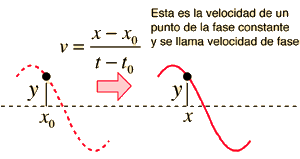
La velocidad de la onda está determinada por las propiedades del medio y es independiente de los otros parámetros, pero puede ser determinada a partir de mediciones de la frecuencia y la longitud de onda. El siguiente cálculo permite especificar cualquiera de las dos cantidades en la relación de onda v = fl y luego iniciar el cálculo haciendo clic en el texto activo de la cantidad que se desea calcular.
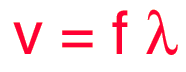
Nota: La posición, velocidad y aceleración se vuelven a calcular, sólo cuando se haga clic en cualquiera de la velocidad, la frecuencia o longitud de onda en la fórmula activa de arriba.
|