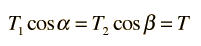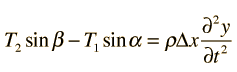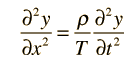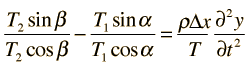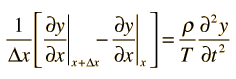La Ecuación de Onda

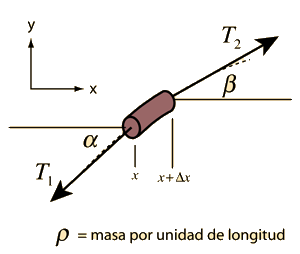
La ecuación de onda de una onda plana de propagación en la dirección x es

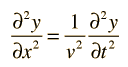
donde v es la velocidad de fase de la onda e y representa la variable que cambia al paso de la onda. Esta es la ecuación de onda que aplica a una cuerda estirada o a una onda electromagnética plana. La descripción matemática de una onda, hace uso de las derivadas parciales.

En dos dimensiones, la ecuación de onda toma la forma

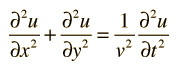
la cual podría describir una onda sobre una membrana estirada.

Ondas en una Cuerda Ideal

La ecuación de onda para una onda en una cuerda ideal se puede obtener aplicando la segunda ley de Newton a un segmento infinitesimal de una cuerda.

Si se mantiene una tensión T constante en la cuerda, entonces la segunda ley de Newton viene a ser La combinación de estas dos expresiones para ángulos pequeños da Mostrar Detalles Soluciones a la ecuación de Onda

Desarrollo de la Ecuación de Onda en una Cuerda

El análisis de las fuerzas sobre un segmento de cuerda estirada da dos relaciones:

Combinando da y relacionando esto con las pendientes en los extremos del segmento, da En el límite Δx→ 0 esto viene a ser Ecuación de Onda

Limitaciones a la Cuerda Ideal

Con objeto de aplicar la ecuación de onda a las ondas en una cuerda, se deben cumplir ciertas condiciones. En una cuerda ideal se asume que

1. La cuerda es perfectamente uniforme con una masa constante por unidad de longitud, y es perfectamente elástica sin ofrecer resistencia a la flexión.

2. La tensión de la cuerda es lo suficientemente grande para poder despreciar los efectos de la gravedad.

3. Se supone que los pequeños segmentos de la cuerda se mueven transversalmente en un plano perpendicular a la cuerda, y que los desplazamientos y pendientes de segmentos son pequeños.

Aunque estrictas, estas idealizaciones permiten el desarrollo de una ecuación de onda que describe así las vibraciones de las cuerdas finas reales.