Ecuaciones Diferenciales

Una ecuación diferencial es una ecuación que contiene derivadas de una variable, como en la ecuación

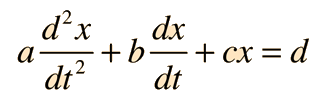
Aquí x es la variable y las derivadas son con respecto a una segunda variable t. Las letras a, b, c y d se toman aquí como constantes. Esta ecuación podría describirse como una ecuación diferencial lineal, de segundo orden, con coeficientes constantes. Es de segundo orden debido al orden mas alto de derivadas presentes, lineal porque ninguna de las derviadas están elevadas a ninguna potencia y los factores multiplicando las derivadas son constantes. Si fuera x la posición de un objeto y t el tiempo, entonces la primera derivada es la velocidad, la segunda la aceleración, y esta podría ser una ecuación describiendo el movimiento de un objeto. Como se muestra, tambien se dice que esta es una ecuación no homogénea, y al resolver problemas físicos, uno debe considerar tambien la ecuación homogénea.

E.D. Homogéneas de Primer Orden

Una ecuación diferencial de primer orden homogénea, implica solamente a la primera derivada de la función, a la función misma, y a coeficientes constantes. La ecuación es de la forma

y puede resolverse por sustitución

La solución que se ajusta a una situación física específica, se obtiene sustituyendo la solución en la ecuación, y evaluando las diversas constantes que se obtienen, al forzar la solución para adaptarse a las condiciones de contorno físico del problema en cuestión. Sustituyendo da

Aplicaciones

Ecuación No Homogénea de Primer Orden

Solución General de las E.D.

Condiciones de Contorno

Teorema de Singularidad

En las ecuaciones diferenciales aplicables a problemas físicos, a menudo es posible comenzar con una forma general de solución y luego forzarla para adaptarse a las condiciones físicas de contorno del problema. Este tipo de enfoque ha sido posible por el hecho de que hay una y sólo una solución a la ecuación diferencial, es decir, la solución es única.

Expresado en términos de una ecuación diferencial de primer orden, si el problema

cumple la condición tal que f (x, y) y la derivada de y es continua en un rectángulo de valores determinados (x, y), entonces hay una y sólo una solución a la ecuación que satisfaga las condiciones de contorno.

Terminología de la Ecuación Diferencial

Algunos términos generales que se usan en el estudio de ecuaciones diferenciales:

Orden: El orden de una ecuación diferencial es la mayor potencia de las derivadas que forman parte de la ecuación, por ejemplo la segunda ley de Newton da lugar a una ecuación diferencial de segundo orden, porque la aceleración es la segunda derivada de la posición.

Lineal y no lineal: Se dice que una ecuación diferencial es lineal si cada término de la ecuación tiene solamente un orden de derivadas, es decir ningún término puede tener ambos y y su derivada respecto del tiempo. Tampoco debe tener ninguna derivada elevada a una potencia.

Homogenea y no homogénea: Una ecuación diferencial se dice que es homogénea si no tiene ningun término que sea un coeficiente aislado, es decir, cada término de la ecuación diferencial de y contiene a y o alguna derivada de y.