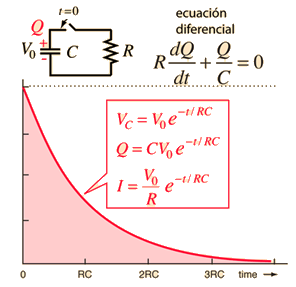
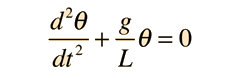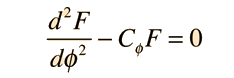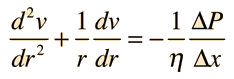E.D. Homogénea de Segundo Orden
Una ecuación diferencial homogénea de segundo orden lineal, lleva términos de hasta la segunda derivada de una función. En el caso de coeficientes constantes, la ecuación tiene la forma
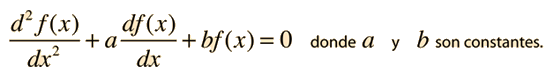
y puede resolverse por sustitución

La solución que se ajusta a la situación física específica, se obtiene sustituyendo la solución en la ecuación, y evaluando los diferentes coeficientes constantes, por medio de forzar la solución para que se adapte a las condiciones de contorno físico del problema en cuestión. Sustituyendo da
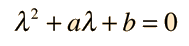
lo cual, lleva a una variedad de soluciones dependiendo de los valores de a y de b. En los problemas físicos, las condiciones de contorno determinan los valores de a y b y la solución a la ecuación cuadrática de λ, revela la naturaleza de la solución.
Caso I: Dos raices reales
Para valores de a y b, tales como
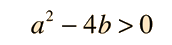
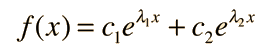
Caso II: Una raiz real doble
Si a y b son tales que
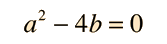
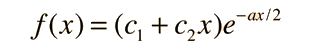
Case III: Raices Complejas Conjugadas
Para valores de a y b tales que
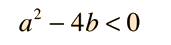

La solución a la ecuación homogénea es por sí misma importante para muchas aplicaciones de física, y también es una parte de la solución de la ecuación no homogénea.
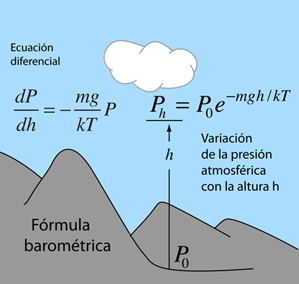
Aplicaciones
| HyperPhysics****HyperMath*****Ecuaciones Diferenciales | M Olmo R Nave |