Ecuación Diferencial No Homogénea de Primer Orden
Un ejemplo de ecuación diferencial no homogénea lineal de primer orden es
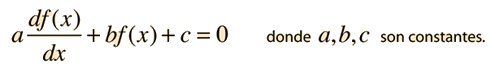
Un valor de la constante c distinto de cero es lo que hace que la ecuacións sea no homogénea y añade un paso mas en el proceso de solución de la misma. El camino hacia una solución general pasa por encontrar previamente una solución a la ecuación homogénea (es decir, quitar la constante c), y luego encontrar una solución particular a la ecuación no homogénea (es decir, encontrar cualquier solución considerando la constante c como parte de la ecuación). La solución a la ecuación homogénea es
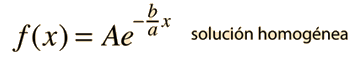
Por sustitución, se puede verificar que estableciando esta función igual al valor constante -c/b satisfacerá a la ecuación no homogénea.

Forma parte de la naturaleza de las ecuaciones diferenciales, que la suma de soluciones sea también otra solución, de modo que tomando la suma de las dos soluciones de arriba, se puede aproximar a una solución general. El requisito final para la aplicación de la solución al problema físico es que la solución encuentre las condiciones de contorno físicas del problema. La situación mas normal en los problemas físicos, es que las condiciones de contorno (condiciones de frontera) son los valores de la función f(x) y sus derivadas cuando x=0. Las condiciones de contorno a menudo se llaman "condiciones iniciales". Para la ecuación de primer orden, necesitamos especificar una condición de contorno. Por ejemplo:
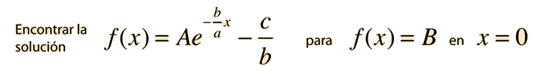
Sustituyendo para x=0 da:
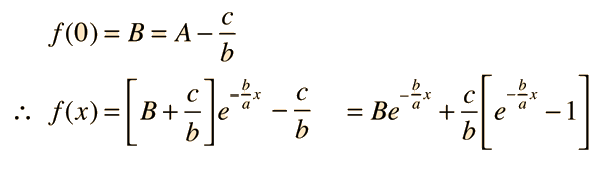
| Ejemplo de la Carga de un Condensador |
| HyperPhysics*****HyperMath*****Ecuaciones Diferenciales | M Olmo R Nave |
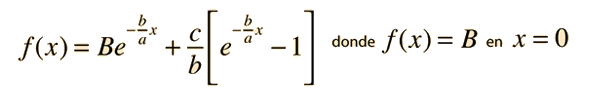 .
.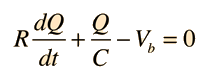 .
. .
.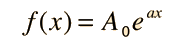 .
. .
. .
.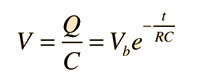 .
.